题目内容
2.若$\frac{5x+1}{6}$与-$\frac{2}{3}$互为倒数,则x的值是-2.分析 首先根据$\frac{5x+1}{6}$与-$\frac{2}{3}$互为倒数,可得$\frac{5x+1}{6}$=-$\frac{3}{2}$,然后根据解一元一次方程的方法,求出x的值是多少即可.
解答 解:∵$\frac{5x+1}{6}$与-$\frac{2}{3}$互为倒数,
∴$\frac{5x+1}{6}$=-$\frac{3}{2}$,
去分母,得5x+1=-9
移项,得5x=-9-1
合并同类项,得5x=-10
系数化为1,得x=-2
∴若$\frac{5x+1}{6}$与-$\frac{2}{3}$互为倒数,则x的值是-2.
故答案为:-2.
点评 此题主要考查了倒数的含义和求法,以及解一元一次方程的方法,要熟练掌握,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.

练习册系列答案
相关题目
4.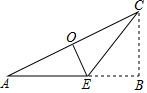 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
7.为测量某特种车辆的性能,研究制定了行驶指数P,P=K+1000,而K的大小与平均速度v(km/h)和行驶路程s(km)有关(不考虑其他因素),K由两部分的和组成,一部分与v2成正比,另一部分与sv成正比.在实验中得到了表格中的数据:
(1)用含v和s的式子表示P;
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
| 速度v | 40 | 60 |
| 路程s | 40 | 70 |
| 指数P | 1000 | 1600 |
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
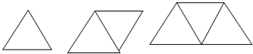 请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.
请你拿出火柴棒,现在我们来用火柴棒搭如图所示的三角形.
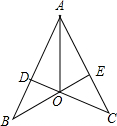 如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且AD=AE,有以下结论:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等,其中正确的结论有( )
如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE与CD相交于点O,且AD=AE,有以下结论:①∠B=∠C,②△ADO≌△AEO;③△BOD≌△COE;④图中有四组三角形全等,其中正确的结论有( ) 实数a,b,c在数轴上的对应点如图所示,化简a+|a+b|-$\sqrt{c^2}$-|b-c|.
实数a,b,c在数轴上的对应点如图所示,化简a+|a+b|-$\sqrt{c^2}$-|b-c|.