题目内容
7.为测量某特种车辆的性能,研究制定了行驶指数P,P=K+1000,而K的大小与平均速度v(km/h)和行驶路程s(km)有关(不考虑其他因素),K由两部分的和组成,一部分与v2成正比,另一部分与sv成正比.在实验中得到了表格中的数据:| 速度v | 40 | 60 |
| 路程s | 40 | 70 |
| 指数P | 1000 | 1600 |
(2)当行驶指数为500,而行驶路程为40时,求平均速度的值;
(3)当行驶路程为180时,若行驶指数值最大,求平均速度的值.
分析 (1)设K=mv2+nsv,则P=mv2+nsv+1000,待定系数法求解可得;
(2)将P=500代入(1)中解析式,解方程可得;
(3)将s=180代入解析式后,配方成顶点式可得最值情况.
解答 解:(1)设K=mv2+nsv,则P=mv2+nsv+1000,
由题意得:$\left\{\begin{array}{l}{4{0}^{2}•m+1600n+1000=1000}\\{6{0}^{2}•m+4200n+1000=1600}\end{array}\right.$,
整理得:$\left\{\begin{array}{l}{m+n=0}\\{6m+7n=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-1}\\{n=1}\end{array}\right.$,
则P=-v2+sv+1000;
(2)根据题意得-v2+40v+1000=500,
整理得:v2-40v-500=0,
解得:v=-10(舍)或v=50,
答:平均速度为50km/h;
(3)当s=180时,P=-v2+180v+1000=-(v-90)2+9100,
∴当v=90时,P最大=9100,
答:若行驶指数值最大,平均速度的值为90km/h.
点评 本题主要考查待定系数法求函数解析式、解二元一次方程组、解一元二次方程的能力及二次函数的性质,熟练掌握待定系数法求得函数解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.一天,昆明的最高气温为6℃,最低气温为-4℃,那么这天的最高气温比最低气温高( )
| A. | 10℃ | B. | -10℃ | C. | 2℃ | D. | -2℃ |
 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)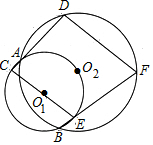 如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.
如图,⊙O1与⊙O2经过A,B两点,过A点的直线与⊙O1交于点C,与⊙O2交于点D,过B点的直线与⊙O1交于点E,与⊙O2交于点F.证明:CE∥DF.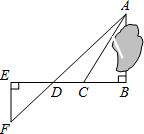 为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号)
为了测量被池塘隔开的A、B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据:①BC,∠ACB; ②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.根据所测数据,能出A,B间距离的有①②③(填上所有能求出A、B间距离的序号) 如图,在⊙O中,∠AOB=46°,则∠ACB=23°.
如图,在⊙O中,∠AOB=46°,则∠ACB=23°.