题目内容
4.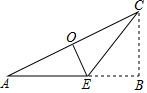 如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )
如图,在Rt△ABC中,点E在AB上,把这个直角三角形沿CE折叠后,使点B恰好落到斜边AC的中点O处,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 由翻折的性质可知,BC=CO=AO=3,推出AC=2BC,在Rt△ACB中,由sin∠A=$\frac{BC}{AC}$=$\frac{1}{2}$,推出∠A=30°,在Rt△AOE中,根据OE=OA•tan30°计算即可.
解答 解:由翻折的性质可知,BC=CO=AO=3,
∴AC=2BC,
在Rt△ACB中,sin∠A=$\frac{BC}{AC}$=$\frac{1}{2}$,
∴∠A=30°,
在Rt△AOE中,OE=OA•tan30°=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$,
∴CE=20E=2$\sqrt{3}$
故选B.
点评 本题考查翻折变换、锐角三角函数等知识,解题的关键是证明∠A=30°,灵活运用三角函数解决问题,属于中考常考题型.

练习册系列答案
相关题目
14.以下问题,不适合用全面调查的是( )
| A. | 了解全班同学每周体育锻炼的时间 | B. | 旅客上飞机前的安检 | ||
| C. | 了解全市中小学生每天的零花钱 | D. | 学校招聘教师,对应聘人员面试 |
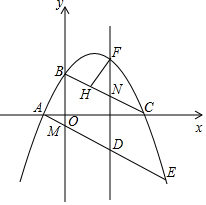 如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N
如图所示,在平面直角坐标系中,抛物线y=ax2+bx+2(a≠0)经过点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点M(0,-$\frac{1}{2}$)为y轴负半轴上的一点,连接AM并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线与抛物线交于点F,与线段BC交于点N 已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C.
已知:如图,在平面直角坐标系xOy中,直线y=-$\frac{3}{4}$x+6与x轴、y轴的交点分别为A、B两点,将∠OBA对折,使点O的对应点H落在直线AB上,折痕交x轴于点C. 如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m)
如图,建筑物AB的高为6m,在其正东方向有一个通信塔CD,在它们之间的地面点M(B,M,D三点在一条直线上)处测得建筑物顶端A,塔顶C的仰角分别为37°和60°,在A处测得塔顶C的仰角为30°,则通信塔CD的高度.(精确到0.01m) 已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.
已知:如图,AB⊥BC于B,CD⊥BC于C,AB=5,BC=8,CD=3,E为线段BC上一点.求:当AE=DE时,BE的长度,并确定此时∠AED的度数.