题目内容
5.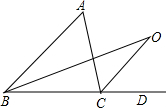 已知,在△ABC中,∠ABC和∠ACD的平分线相交于点O,
已知,在△ABC中,∠ABC和∠ACD的平分线相交于点O,(1)若∠A=70°,则∠BOC=35°;
(2)若∠A=80°,则∠BOC=40°;
(3)试探索:∠BOC和∠A的关系,证明你的结论.
分析 (1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,再根据角平分线的定义表示出∠OBC和∠OCD,然后整理得到∠BOC=$\frac{1}{2}$∠A,代入数据进行计算即可得解;
(2)代入∠BOC=$\frac{1}{2}$∠A求出即可;
(3)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠ACD和∠OCD,再根据角平分线的定义表示出∠OBC和∠OCD,然后整理得到∠BOC=$\frac{1}{2}$∠A,代入数据进行计算即可得解.
解答 解:(1)由三角形外角性质,∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,
∵BO、CO分别平分∠ABC和∠ACD,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCD=$\frac{1}{2}$∠ACD,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠BOC,
∴∠BOC=$\frac{1}{2}$∠A,
∵∠A=70°,
∴∠BOC=35°,
故答案为:35°;
(2)由(1)知:∠BOC=$\frac{1}{2}$∠A,
∵∠A=80°,
∴∠BOC=40°,
故答案为:40°;
(3)∠BOC=$\frac{1}{2}$∠A;
理由是:由三角形外角性质,∠ACD=∠A+∠ABC,∠OCD=∠OBC+∠BOC,
∵BO、CO分别平分∠ABC和∠ACD,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCD=$\frac{1}{2}$∠ACD,
∴$\frac{1}{2}$∠A+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ABC+∠BOC,
∴∠BOC=$\frac{1}{2}$∠A.
点评 本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.

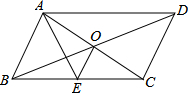 如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )
如图,?ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④∠COD=60°,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
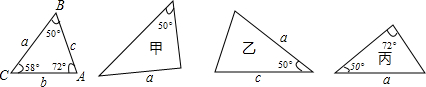
| A. | 只有乙 | B. | 只有丙 | C. | 甲和乙 | D. | 乙和丙 |
| A. | $\sqrt{\frac{1}{x-2}}$ | B. | $\sqrt{x-2}$ | C. | $\sqrt{\frac{1}{x+2}}$ | D. | $\sqrt{x+2}$ |
