题目内容
1．若抛物线y=2（x-2）2+k过原点，则该抛物线与x轴的另一个交点坐标为（4，0）．分析 利用抛物线的对称性求解．
解答 解：∵抛物线的对称轴为直线x=2，
而抛物线过原点，
∴抛物线与x轴的另一个交点坐标为（4，0）．
故答案为（4，0）．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标转化为解关于x的一元二次方程．
练习册系列答案
相关题目
尺规作图：
9．已知：$\frac{x+y}{x-2y}=\frac{5}{2}$，则$\frac{x}{y}$的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | 3 | D． | 4 |
16．
已知二次函数y=2x2+4x-6．
（1）把函数配成y=a（x-h）2+k的形式；
（2）求函数与x轴交点坐标；
（3）用五点法画函数图象
根据图象回答：
（4）当y≥0时，则x的取值范围为x≥1或x≤-3．
（5）当-3＜x＜0时，则y的取值范围为0＞y≥-8．
已知二次函数y=2x2+4x-6．（1）把函数配成y=a（x-h）2+k的形式；
（2）求函数与x轴交点坐标；
（3）用五点法画函数图象
| x | … | … | |||||
| y | … | … |
（4）当y≥0时，则x的取值范围为x≥1或x≤-3．
（5）当-3＜x＜0时，则y的取值范围为0＞y≥-8．
11．
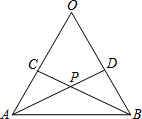如图所示，AO=BO，CO=DO，连接AD、BC，设AD、BC相交于点P．结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．以上结论中（ ）
如图所示，AO=BO，CO=DO，连接AD、BC，设AD、BC相交于点P．结论：①△AOD≌△BOC；②△APC≌△BPD；③点P在∠AOB的平分线上．以上结论中（ ）| A． | 只有①正确 | B． | 只有②正确 | C． | 只有①②正确 | D． | ①②③都正确 |