��Ŀ����
15����֪����ABC����BC=AB����ABC=90�㣬A����x��ĸ������ϣ�ֱ�Ƕ���B��y���ϣ���C��x���Ϸ�����1����ͼ1��ʾ����A�������ǣ�-3��0������B��ԭ���غϣ����C�������ǣ�0��3����
��2����ͼ2������C��CD��y����D�����ж��߶�OA��OD��CD֮���������ϵ��˵�����ɣ�
��3����ͼ3����x��ǡ��ƽ�֡�BAC��BC��x�ύ�ڵ�E������C��CF��x���ڵ�F����CF��AE��������������ϵ����˵�����ɣ�

���� ��1�����ݵ�A��-3��0����BC=BA�ɵõ�C���ꣻ
��2��OA=OD+CD��֤����ABO�ա�BCD���õ�BO=CD��OA=DB�����ɽ��
��3��AE=2CF����ͼ3���ӳ�CF��AB�ཻ��G��֤����AFC�ա�AFG���õ�CF=GF����֤����ABE�ա�CBG���õ�AE=CG�����ɽ��
��� �⣺��1����BC=AB����A�������ǣ�-3��0����
��BC=BA=3��
���C��������0��3����
�ʴ�Ϊ����0��3����
��2��OA=OD+CD��
��CD��y�ᣬ
���CDB=90�㣬��DCB+��CBD=90�㣬
�ߡ�ABC=90�㣬
���ABO+��CBD=90�㣬
���ABO=��DCB��
�ڡ�ABO�͡�BCD�У�
��$\left\{\begin{array}{l}{��ABO=��DCB}\\{��AOB=��BDC=90��}\\{AB=CB}\end{array}\right.$
���ABO�ա�BCD��
��BO=CD��OA=DB��
��BD=OB+OD��
��OA=CD+OD��
��3��AE=2CF��
��ͼ3���ӳ�CF��AB�ཻ��G��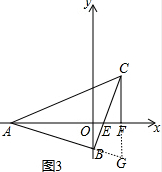
��x��ǡ��ƽ�֡�BAC��
���CAF=��GAF��
��CF��x�ᣬ
���AFE=��AFG=90�㣬
�ڡ�AFC�͡�AFG�У�
��$\left\{\begin{array}{l}{��CAF=��GAF}\\{AF=AF}\\{��AFC=��AFG}\end{array}\right.$��
���AFC�ա�AFG��
��CF=GF��
�ߡ�AEB=��CEF����ABE=��CFE=90�㣬
���BAE=��BCG��
�ڡ�ABE�͡�CBG�У�
��$\left\{\begin{array}{l}{��BAO=��BCG}\\{AB=CB}\\{��ABE=��CBG}\end{array}\right.$��
���ABE�ա�CBG��
��AE=CG��
��AE=CF+GF=2CF
���� ���⿼����ȫ�������ε����ʶ������ж��������������Ĺؼ���֤��������ȫ�ȣ�������ȫ�������ε����ʵõ���ȵ��߶Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�| A�� | 626 | B�� | 288 | C�� | 168 | D�� | 624 |
| A�� | 1 | B�� | 2$\sqrt{2}$ | C�� | ��1 | D�� | $��2\sqrt{2}$ |
| A�� | Խ��Խ�ӽ�1 | B�� | Խ��Խ�ӽ�0 | ||
| C�� | û��ʲô���ԵĹ��� | D�� | Խ��Խ�� |
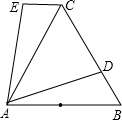 ��ͼ����ABCΪ�ȱ������Σ�D��BC����һ�㣬AB=10��AD=9����ABD������ת60����ACE��λ�ã�
��ͼ����ABCΪ�ȱ������Σ�D��BC����һ�㣬AB=10��AD=9����ABD������ת60����ACE��λ�ã� ��ͼ����ABC�ǵȱ������Σ���D��BC���ϣ�����ABD�Ƶ�A����ʱ�뷽����ת�õ���ACE������DE����ͼ�����BAD��ȵĽǣ�����CAE�⣬���нǡ�EDC������������ĸ��ʾ�ýǣ�
��ͼ����ABC�ǵȱ������Σ���D��BC���ϣ�����ABD�Ƶ�A����ʱ�뷽����ת�õ���ACE������DE����ͼ�����BAD��ȵĽǣ�����CAE�⣬���нǡ�EDC������������ĸ��ʾ�ýǣ�