题目内容
3.在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).(1)点($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$)的“双角坐标”为(60°,60°);
(2)若点P到x轴的距离为$\frac{1}{2}$,则m+n的最小值为90.
分析 (1)分别求出tan∠POA、tan∠PAO即可得∠POA、∠PAO的度数,从而得出答案;
(2)根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,则∠OPA需取得最大值,OA中点为圆心,$\frac{1}{2}$为半径画圆,与直线y=$\frac{1}{2}$相切于点P,由∠OPA=∠1>∠OP′A知此时∠OPA最大,∠OPA=90°,即可得出答案.
解答 解:(1)∵P($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),OA=1,
∴tan∠POA=$\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}}$=$\sqrt{3}$,tan∠PAO=$\frac{\frac{\sqrt{3}}{2}}{1-\frac{1}{2}}$=$\sqrt{3}$,
∴∠POA=60°,∠PAO=60°,
即点P的“双角坐标”为(60°,60°),
故答案为:(60°,60°);
(2)根据三角形内角和定理知若要使m+n取得最小值,即∠POA+∠PAO取得最小值,
则∠OPA需取得最大值,
如图,
∵点P到x轴的距离为$\frac{1}{2}$,OA=1,
∴OA中点为圆心,$\frac{1}{2}$为半径画圆,与直线y=$\frac{1}{2}$相切于点P,
在直线y=$\frac{1}{2}$上任取一点P′,连接P′O、P′A,P′O交圆于点Q,
∵∠OPA=∠1>∠OP′A,
此时∠OPA最大,∠OPA=90°,
∴m+n的最小值为90,
故答案为:90.
点评 本题主要考查坐标与图形的性质、锐角的三角函数、三角形的内角和定理、外角的性质及圆周角定理,根据内角和定理推出m+n取得最小值即为∠OPA取得最大值,且找到满足条件的点P位置是关键.

 阅读快车系列答案
阅读快车系列答案 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,BD=7cm,AD=6cm,则BE的长是( )
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=8cm,BD=7cm,AD=6cm,则BE的长是( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
 如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )
如图,梯形ABCD中,AD∥BC,DE∥AB交BC边于点E.那么下列事件中属于随机事件的是( )| A. | $\overrightarrow{AD}$=$\overrightarrow{EB}$ | B. | $\overrightarrow{AB}$=$\overrightarrow{DC}$ | C. | $\overrightarrow{AB}$=$\overrightarrow{DE}$ | D. | $\overrightarrow{AD}$=$\overrightarrow{EC}$ |
 如图,∠1是三角形的一个外角,则∠1的角度为( )
如图,∠1是三角形的一个外角,则∠1的角度为( )| A. | 85° | B. | 95° | C. | 105° | D. | 75° |
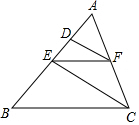 如图EF∥BC,DF∥CE,求证:AE2=AD•AB.
如图EF∥BC,DF∥CE,求证:AE2=AD•AB. 如图,点C在以AB为直径的半圆O上,∠BAC=20°,则∠BOC的度数是40°.
如图,点C在以AB为直径的半圆O上,∠BAC=20°,则∠BOC的度数是40°.