题目内容
12.计算:(1)(x+2)(x-2)+x2(x-1);
(2)[a(a2b2-ab)-b(a2-a3b)]÷3a2b;
(3)($\frac{x}{x+y}$+$\frac{2y}{x+y}$)•$\frac{xy}{x+2y}$•($\frac{1}{x}$+$\frac{1}{y}$)2.
分析 根据整式的运算法则以及分式的运算法则即可求出答案.
解答 解:(1)原式=x2-4+x3-x2
=x3-4
(2)解:原式=(2a3b2-2a2b)÷3a2b
=$\frac{2}{3}$ab-$\frac{2}{3}$
(3)原式=$\frac{x+2y}{x+y}$×$\frac{xy}{x+2y}$×$\frac{(x+y)^{2}}{{x}^{2}{y}^{2}}$
=$\frac{x+y}{xy}$
点评 本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
1.下列选项中,是二元一次方程组的是( )
| A. | x+2y=3 | B. | $\frac{x+5}{3}$-1=x+3 | ||
| C. | $\left\{\begin{array}{l}{x+3y=10}\\{2x+y=16}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x-2y=-9}\\{y-z=3}\\{2z+x=47}\end{array}\right.$ |
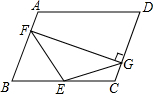 如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)
如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)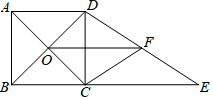 如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.
如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.