题目内容
2.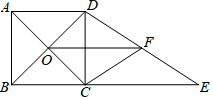 如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.
如图,正方形ABCD的对角线相交于点O,BC=6,延长BC至点E,使得CE=8,点F是DE的中点,连接CF、OF.(1)求OF的长.
(2)求CF的长.
分析 (1)只要证明OF是△DBE的中位线即可解决问题;
(2)在Rt△DCE中,利用勾股定理求出DE,再利用斜边中线的性质即可解决问题;
解答 解:(1)∵ 四边形ABCD是正方形,
四边形ABCD是正方形,
∴BC=CD=6,∠BCD=∠ECD=90°,OB=OD,
∵CE=8,
∴BE=14,
∵OB=OD,DF=FE,
∴OF=$\frac{1}{2}$BE=7.
(2)在Rt△DCE中,DE=$\sqrt{C{D}^{2}+C{E}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵DF=FE,
∴CF=$\frac{1}{2}$DE=5.
点评 本题考查正方形的性质、三角形的中位线定理、直角三角形斜边中线定理、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
17.下列计算中,正确的是( )
| A. | $\sqrt{18}$÷$\sqrt{2}$=$\sqrt{6}$ | B. | (4$\sqrt{2}$)2=8 | C. | $\sqrt{(-2)^{2}}$=2 | D. | 2$\sqrt{3}$×2$\sqrt{2}$=2$\sqrt{6}$ |
7.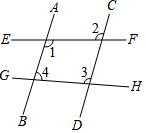 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )
 如图,下列判断中正确的是( )
如图,下列判断中正确的是( )| A. | 如果EF∥GH,那么∠4+∠3=180° | B. | 如果AB∥CD,那么∠1+∠4=180° | ||
| C. | 如果AB∥CD,那么∠1=∠2 | D. | 如果AB∥CD,那么∠2=∠3 |
14.二元一次方程x+2y=10的所有正整数解有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列说法中正确的是( )
| A. | 两条射线所组成的图形叫角 | |
| B. | 角的大小与所画的角的边的长短无关 | |
| C. | 角的两边是两条线段 | |
| D. | 角的两边是两条直线 |
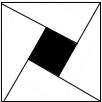 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为4-2$\sqrt{3}$.
由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的边长为1,则图中阴影部分的面积为4-2$\sqrt{3}$. 如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n)
如图反比例函数y=$\frac{k}{x}$的图象与一次函数y=kx+b的图象交于点A(1,4),点B(-4,n)