题目内容
20.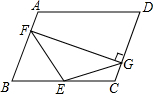 如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)
如图,?ABCD中,∠B=70°,点E是BC的中点,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①EF=EG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°,则正确的结论是①②⑤.(填序号即可)
分析 延长GE交AB的延长线于点H,EO⊥GF与点O,易证得EF=EH=EG,当AD沿着BA、CD移动仍满足题中条件.所以③错误.由等腰三角形的性质以及直角的性质可求得结论.
解答  解:延长GE交AB的延长线于点H,如图,
解:延长GE交AB的延长线于点H,如图,
∵?ABCD中AB∥CD,
∴∠H=∠EGC,
在△BEH和△CEG中,
$\left\{\begin{array}{l}{∠BEH=∠CEG}\\{∠H=∠EGC}\\{BE=CE}\end{array}\right.$,
∴△BEH≌△CEG(AAS),
∴HE=EG,
又∵AB∥CD,FG⊥CD,
∴FG⊥AB,即∠HFG=90°
∴EF=EH=EG,故①正确;
又∵BF=BE=EC,AB=CD,
∴只有当GC=AF时,CE=DG,
但GC不一定等于AF,故③错误.
∵∠FBE=70°,BF=BE,
∴∠BFE=55°
又∵∠BFG=90°,
∴∠EFG=35°,故②正确.
∵EF=EG,
∴∠EFG=∠EGF=35°,
∴∠FEG=180°-35°-35°=110°,故④错误.
∵∠FGC=90°,
∴∠EGC=55°,故⑤正确.
故①②⑤正确;
故答案为:①②⑤.
点评 此题主要考查了平行四边形的性质和应用,要熟练掌握,解答此题的关键是要明确:平行四边形的性质:①边:平行四边形的对边相等.②角:平行四边形的对角相等.③对角线:平行四边形的对角线互相平分,此题还考查了直角三角形的性质,直角三角形斜边上的中线等于斜边的一半,正确作出辅助线是关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
10.在实数$\sqrt{3}$,-2,0,$-\sqrt{2}$中,最大值是( )
| A. | $\sqrt{3}$ | B. | -2 | C. | 0 | D. | $-\sqrt{2}$ |
8.下列各式中计算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$ | B. | 2+$\sqrt{2}$=2$\sqrt{2}$ | C. | $\frac{\sqrt{12}-\sqrt{10}}{2}$=$\sqrt{6}-\sqrt{5}$ | D. | $\sqrt{2}+\sqrt{3}$=$\sqrt{5}$ |
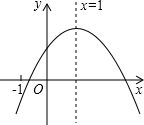 二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( )
二次函数的图象如图所示,对称轴为x=1,给出下列结论:①abc<0;②b2>4ac;③4a+2b+c<0;④2a+b=0.其中正确的结论有( ) 解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来.
解不等式7+x≥2(2x-1),并把解集在如图的数轴上表示出来.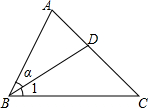 老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D.
老师提出了以下问题:请用恰当的方法表示图中给出的所有角(小于平角的角),某组同学在本组展示区的答案是:∠1、∠α、∠BAD、∠C、∠D.