题目内容
11.若$\sqrt{{a}^{2}-3a+1}$+b2+2b+1=0,求a2+$\frac{1}{{a}^{2}}$+|b|的值.分析 首先把$\sqrt{{a}^{2}-3a+1}$+b2+2b+1=0化为$\sqrt{{a}^{2}-3a+1}$+(b+1)2=0,利用非负数的性质得出a2-3a+1=0,b=-1,进一步整理变形代入求得答案即可.
解答 解:∵$\sqrt{{a}^{2}-3a+1}$+b2+2b+1=0,
∴$\sqrt{{a}^{2}-3a+1}$+(b+1)2=0,
∴a2-3a+1=0,b=-1,
∴a2+$\frac{1}{{a}^{2}}$=3,
∴a2+$\frac{1}{{a}^{2}}$+|b|=3+1=4.
点评 此题考查配方法的运用,非负数的性质,由a2-3a+1=0变形得出a2+$\frac{1}{{a}^{2}}$=3是解决问题的关键.

练习册系列答案
相关题目
19.根据物理学规律,如果把一物体从地面以10m/s的速度竖直上抛,那么经过x s物体离地面的高度(单位:m)为10x-4.9x2.根据上述规律.则物体经过$\frac{100}{49}$s落回地面.
16.计算:-$\frac{4}{5}$×(10-1$\frac{1}{4}$+0.5)=-8+1-0.4,这个运算应用了( )
| A. | 加法结合律 | B. | 乘法结合律 | C. | 乘法交换律 | D. | 乘法分配律 |
 如图△ABC≌△A′B′C′,AA′∥BC,∠ABC=70°,求∠CBC′的大小.
如图△ABC≌△A′B′C′,AA′∥BC,∠ABC=70°,求∠CBC′的大小.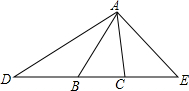 如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形.
如图,△ABC中,∠ACB=80°,延长CB至D,使DB=BA,延长BC至E,使CE=CA.连接AD,AE,若∠DAE=115°,试说明△ABC是等腰三角形.