题目内容
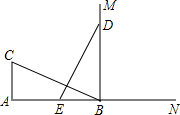 如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过考点:全等三角形的判定
专题:动点型
分析:设点E经过t秒时,△DEB≌△BCA;由斜边ED=CB,分类讨论BE=AC或BE=AB时的情况,求出t的值即可.
解答:解:设点E经过t秒时,△DEB≌△BCA;此时AE=3t
分情况讨论:(1)当点E在点B的左侧时,
BE=24-3t=12,
∴t=4;
(2)当点E在点B的右侧时,
①BE=AC时,3t=24+12,
∴t=12;
②BE=AB时,
3t=24+24,
∴t=16.
综上所述,故答案为:4,12,16.
分情况讨论:(1)当点E在点B的左侧时,
BE=24-3t=12,
∴t=4;
(2)当点E在点B的右侧时,
①BE=AC时,3t=24+12,
∴t=12;
②BE=AB时,
3t=24+24,
∴t=16.
综上所述,故答案为:4,12,16.
点评:本题考查了全等三角形的判定方法;分类讨论各种情况下的三角形全等是解决问题的关键.

练习册系列答案
相关题目
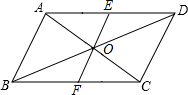 如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:
如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证: 如图:⊙O1和⊙O2是等圆,P是O1O2的中点.过点P作直线AD交⊙O1于点A、B,交⊙O2于点C、D,求证:AB=CD.
如图:⊙O1和⊙O2是等圆,P是O1O2的中点.过点P作直线AD交⊙O1于点A、B,交⊙O2于点C、D,求证:AB=CD.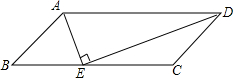 如图,?ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论:①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的个数是( )
如图,?ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论:①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的个数是( )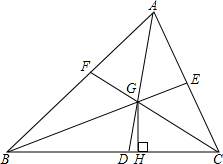 如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.
如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由. 如图,直径AB⊥CD于E,∠COB=α,则
如图,直径AB⊥CD于E,∠COB=α,则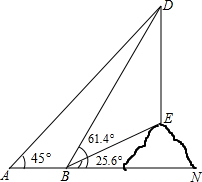 如图,课外数学活动小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直,他们在A处测塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,塔底E的仰角∠EBN=25.6°,现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8)
如图,课外数学活动小组要测量小山坡上塔的高度DE,DE所在直线与水平线AN垂直,他们在A处测塔尖D的仰角为45°,再沿着射线AN方向前进50米到达B处,此时测得塔尖D的仰角∠DBN=61.4°,塔底E的仰角∠EBN=25.6°,现在请你帮助课外活动小组算一算塔高DE大约是多少米?(结果精确到个位)(参考数据:sin25.6°≈0.4,cos25.6°≈0.9,tan25.6°≈0.5,sin61.4°≈0.9,cos61.4°≈0.5,tan61.4°≈1.8) 如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长.
如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长. 已知:如图
已知:如图