题目内容
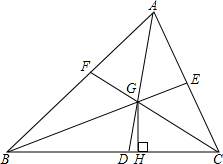 如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.
如图,在△ABC中,AD,BE,CF是角平分线,交点是点G,GH⊥BC,试说明∠BGD=∠CGH的理由.考点:三角形内角和定理,三角形的外角性质
专题:
分析:如图,证明∠ABC+∠BCA+∠CAB=180°,得到2(α+β+γ)=180°,进而得到α+β=90°-γ;证明∠BGD=α+β,∠CGH=90°-γ,即可解决问题.
解答: 证明:如图,∵AD,BE,CF是角平分线,
证明:如图,∵AD,BE,CF是角平分线,
∴∠BAG=∠CAG(设为α),∠ABG=∠CBG(设为β),
∠DCG=∠ACG(设为γ);
∵∠ABC+∠BCA+∠CAB=180°,
∴2(α+β+γ)=180°,
∴α+β+γ=90°,
∴α+β=90°-γ;
∵∠BGD=α+β,∠CGH=90°-γ,
∴∠BGD=∠CGH.
 证明:如图,∵AD,BE,CF是角平分线,
证明:如图,∵AD,BE,CF是角平分线,∴∠BAG=∠CAG(设为α),∠ABG=∠CBG(设为β),
∠DCG=∠ACG(设为γ);
∵∠ABC+∠BCA+∠CAB=180°,
∴2(α+β+γ)=180°,
∴α+β+γ=90°,
∴α+β=90°-γ;
∵∠BGD=α+β,∠CGH=90°-γ,
∴∠BGD=∠CGH.
点评:该题主要考查了三角形的内角和定理、外角的性质及其应用问题;解题的关键是牢固掌握三角形的内角和定理、外角的性质,这是灵活运用的基础和关键.

练习册系列答案
相关题目
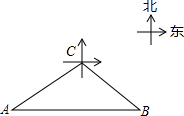 已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,
已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50, 如图,北部湾海面有一艘某军的军舰正在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东60°方向.且在B的北偏西30°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时)(
如图,北部湾海面有一艘某军的军舰正在基地A的正东方向且距A地60海里的B处训练,突然接到基地命令,要该舰前往C岛,接送一名病危的渔民到基地医院救治.已知C岛在A的北偏东60°方向.且在B的北偏西30°方向,军舰从B处出发,平均每小时行驶20海里,需要多少时间才能把患病渔民送到基地医院.(精确到0.1小时)(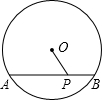 如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB=
如图,AB是⊙O的弦,P是线段AB上一动点,OP长度满足2≤OP≤3,则AB= 如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.
如图,已知∠A=60°,∠B=∠D=90°,AB=2,CD=1,求BC和AD的长.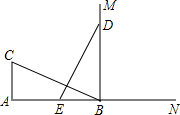 如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
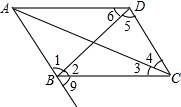 如图,若∠2=∠6,则
如图,若∠2=∠6,则 如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由.
如图,已知∠1与∠2互补,∠1与∠3相等,那么AB和CD平行吗?EF和CH平行吗?说明理由.