题目内容
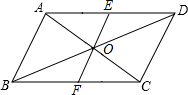 如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:
如图,在?ABCD中,AC,BD交于点O,E是AD的中点,EO的延长线交BC于点F.求证:(1)F是BC的中点;
(2)OE=OF.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用平行四边的性质借助全等三角形的判定方法以及其性质求出即可;
(2)利用全等三角形的性质求出即可.
(2)利用全等三角形的性质求出即可.
解答:证明:(1)∵在?ABCD中,AC,BD交于点O,
∴BO=DO,AD∥BC,AD=BC,
∴∠ADB=∠CBD,
在△DEO和△BFO中
,
∴△DEO≌△BFO(ASA),
∴BF=DE,
∵AE=DE,
∴BF=AE=DE=
BC,
故F是BC的中点;
(2)∵△DEO≌△BFO,
∴EO=FO.
∴BO=DO,AD∥BC,AD=BC,
∴∠ADB=∠CBD,
在△DEO和△BFO中
|
∴△DEO≌△BFO(ASA),
∴BF=DE,
∵AE=DE,
∴BF=AE=DE=
| 1 |
| 2 |
故F是BC的中点;
(2)∵△DEO≌△BFO,
∴EO=FO.
点评:此题主要考查了平行四边的性质以及全等三角形的判定方法以及其性质等知识,得出△DEO≌△BFO是解题关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
经专家估算,整个南海属于我国海疆线以内的油气资源约合1500忆美元,开采前景甚至要超过英国的北海油田,用科学记数法表示15000亿美元是( )
| A、1.5×104美元 |
| B、1.5×105美元 |
| C、1.5×1012 美元 |
| D、1.5×1013美元 |
 如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E,求证:BD=BE.
如图,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E,求证:BD=BE.
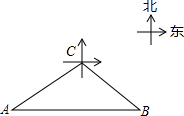 已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50,
已知一艘轮船从港口A出发以80km∕h的速度向正东方向航行,30min后到港口B,又从港口B以同样的速度15min后航行到港口C,此时在C处测得港口A位于港口C的南偏西63.4°方向上,求该艘轮船以80km∕h的速度返回到港口A所需的时间.(精确到0.01h,参考数据:cos63.4°≈0.45,sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50, 如图,O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=2cm,若△ABC得周长是31cm,求△ABC的面积.
如图,O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=2cm,若△ABC得周长是31cm,求△ABC的面积.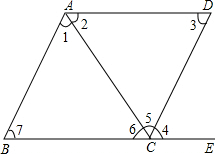 如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
如图,请分别根据已知条件进行推理,得出结论,并在括号内注明理由.
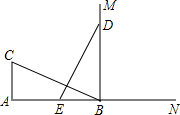 如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过