题目内容
 如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长.
如图,在?ABCD中,CE平分∠BCD交AB于E,DF平分∠ADC交AB于F,若AB=6,BC=4,求EF的长.考点:平行四边形的性质
专题:
分析:首先根据平行四边形的性质可得CD∥AB,再根据角平分线的性质可得∠ECB=∠DCE,然后证明BC=BE,AD=AF,进而可得AF+FB+EF=8,再由AB=6可得答案.
解答:解:∵四边形ABCD是平行四边形,
∴CD∥AB,AD=BC=4,
∴∠DCE=∠BEC,
∵CE平分∠BCD交AB于E,
∴∠ECB=∠DCE,
∴∠ECB=∠CEB,
∴BE=CB=4,
同理:AF=AD=4,
∴AF+EB=8,
∴AF+FB+EF=8,
∵AB=6,
∴EF=2.
∴CD∥AB,AD=BC=4,
∴∠DCE=∠BEC,
∵CE平分∠BCD交AB于E,
∴∠ECB=∠DCE,
∴∠ECB=∠CEB,
∴BE=CB=4,
同理:AF=AD=4,
∴AF+EB=8,
∴AF+FB+EF=8,
∵AB=6,
∴EF=2.
点评:此题主要考查了平行四边形的性质和角平分线的性质,关键是掌握平行四边形对边平行且相等.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
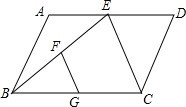 如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )
如图,?ABCD中,点E是AD边上的一个动点,FG是△BCE的中位线,在点E从A运动到D的过程中,FG与△BCE的面积变化分别为( )| A、FG的长度不变,△BCE的面积也不改变 |
| B、FG的长度逐渐变大,△BCE的面积逐渐减小 |
| C、FG的长度先变大再变小,△BCE的面积逐渐变大 |
| D、FG的长度先变小再变大,△BCE的面积不改变 |
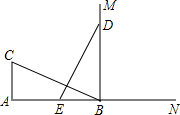 如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过
如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过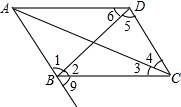 如图,若∠2=∠6,则
如图,若∠2=∠6,则 一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形)
一个物体的主视图如图所示,请你画出这个物体的俯视图(要求分别画出三种不同的情形)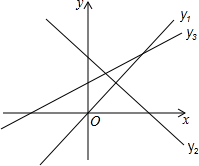 如图,已知直线y1=x,y2=-x+2,y3=
如图,已知直线y1=x,y2=-x+2,y3= 如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1=
如图,在△ABC中,∠C=90°,DE垂直平分AB,交AB于点E,交BC于点D,∠1= 如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形.
如图,已知线段AB平移后的位置点C,作出线段AB平移后的图形.