题目内容
2.已知a、b、c都为正数,且任意两数之和大于第三数,判断式子4a2b2-(a2-c2+b2)2值的正负,并说明理由.分析 将原式用平方差公式分解,再将每个括号内配成完全平方式,然后再用平方差分解后根据任意两数之和大于第三数即可判断.
解答 解:式子4a2b2-(a2-c2+b2)2值为正
原式=(2ab+a2-c2+b2)(2ab-a2+c2-b2)
=[(a+b)2-c2][c2-(a-b)2]
=(a+b-c)(a+b+c)(c-a+b)(c+a-b)
由题设,∵a、b、c均大于0,且有任意两个数之和大于第三数
∴4b2c2-(b2+c2-a2)2是个正数.
点评 本题主要考查因式分解的应用,熟练掌握完全平方公式和平方差公式是根本和关键,将原式依据题意分解成两数之和与第三数间的关系式是切入点.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
10.小明从家出发,先向东走350m到小亮家,然后它们又向南走500m到老师家,如果以老师家的位置为平面直角坐标系的坐标原点,正东方向为x轴正方向为x轴正方向,正北方向为y轴正方向,那么小明家的位置可记为( )
| A. | (350,500) | B. | (-350,-500) | C. | (350,-500) | D. | (-350,500) |
7.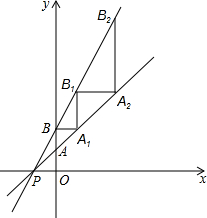 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
 如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )
如图,直线y=x+1交x轴、y轴分别于P、A两点,直线y=2x+2交y轴于B点,过B作x轴的平行线交直线PA于A1,过A1作y轴的平行线交直线PB于B1,过B1作x轴的平行线交直线PA于A2,…如此反复,则A6的坐标为( )| A. | (63,64) | B. | (65,64) | C. | (31,32) | D. | (127,128) |
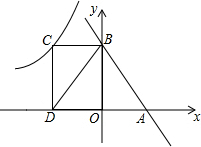 如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6.
如图,直线y=-x+2与x轴、y轴分别交于A、B两点,过B点作BC⊥y轴与双曲线y=$\frac{k}{x}$(k<0)交于C点,过C作CD⊥x轴于D.若△BOD的面积为3,则k的值为-6. 如图,在四边形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,AB=2,CD=6,则四边形ABCD的面积为24.
如图,在四边形ABCD中,AB∥CD,AD=BC,对角线AC⊥BD,AB=2,CD=6,则四边形ABCD的面积为24.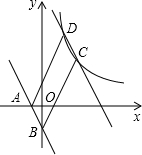 如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),
如图,直线AB:y=kx+b(k≠0)过点A(-1,0)和B(0,-2),