题目内容
12.某工程指挥部,要对某路段工程进行施工,现有甲、乙两个工程队,已知甲队单独完成这项工程所需天数是乙单独完成这项工程所需天数的$\frac{2}{3}$;若由甲队先做20天,剩下的工程再由甲、乙两队合作24天可以完成.(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为0.8万元,乙队每天的施工费用为0.6万元,该工程的工程预算款不超过50万元,工程期限要求不超过40天,在施工中,由于乙队先有其他任务需要完成,先由甲队独立施工了若干天,然后由甲、乙两队合作完成余下的工程,问此项工程能否在计划的工期和工程预算下顺利完工?若能求出甲先独立完成的天数,若不能说明理由.
分析 (1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要$\frac{2}{3}$x天,根据由甲队先做20天,剩下的工程再由甲、乙两队合作24天可以完成任务列方程求解即可;
(2)设甲对先独立完成了x,两队合作了y天,根据工程的工程预算款不超过50万元;工程期限要求不超过40天;恰好能完成整个工程列出不等式组即可求得甲先独立完成的天数.
解答 解:(1)设乙队单独完成这项工程需要x天,则甲队单独完成这项工程需要$\frac{2}{3}$x天.
根据题意得:20×$\frac{3}{2x}$+24×($\frac{1}{x}$$+\frac{3}{2x}$)=1.
解得:x=90.
经检验x=90是原分式方程的解.
$\frac{2}{3}$x=90×$\frac{2}{3}$=60.
答:乙队单独完成这项工程需要90天,则甲队单独完成这项工程需要60天.
(2)能.
理由:设甲对先独立完成了x,两队合作了y天.
根据题意得:0.8x+1.4y≤50①,x+y≤40②,$\frac{x+y}{60}+\frac{y}{90}=1$③.
由③得:y=$\frac{180-3x}{5}$④.
将④代入①得:0.8x+1.4×($\frac{180-3x}{5}$)≤50⑤,
将④代入②得:x+$\frac{180-3x}{5}$≤40⑥.
解不等式⑤得:x≥10,
解不等式⑥得:x≤10.
所以x=10.
答:甲先独立完成10天.
点评 此题主要考查了分式方程的应用、一元一次不等式组的应用,根据题意列出方程或不等式组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.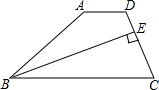 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
 如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )
如图,在四边形ABCD中,AD∥BC,BE平分∠ABC交CD于E,且BE⊥CD,CE:ED=2:1.如果△BEC的面积为2,那么四边形ABED的面积是( )| A. | $\frac{7}{4}$ | B. | $\frac{5}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{2}{3}$ |
7.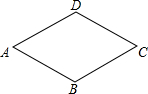 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
 如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )
如图,菱形ABCD中,∠A=60°,周长是16,则菱形的面积是( )| A. | 16 | B. | 16$\sqrt{2}$ | C. | 16$\sqrt{3}$ | D. | 8$\sqrt{3}$ |
4.在平面直角坐标系中,第四象限内有一点P,且P点到x轴距离是4,到y轴的距离是5,则点P点坐标为( )
| A. | (4,5) | B. | (4,-5) | C. | (5,4) | D. | (5,-4) |
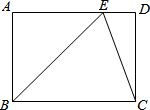 如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.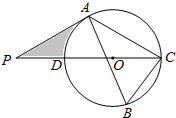 如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.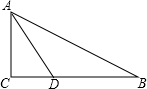 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,CD=3,BD=5,求AC的长.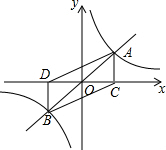 如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.
如图,函数y=x与y=$\frac{4}{x}$的图象相交于A、B两点,过A、B两点分别作x轴垂线,垂足分别为点C、D,则四边形ACBD的面积为8.