题目内容
6.如图①,将两个完全相同的三角板纸片ABC与DEC重合放置,其中∠C=90°,∠B=∠E=30°.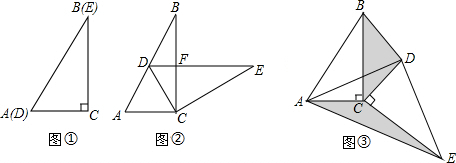
(1)如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,DE交BC于点F,则线段DF与AC有怎样的关系?请说明理由.
(2)当△DEC绕点C旋转到图③的位置时,设△BDC的面积为S1,△AEC中的面积为S2,猜想:S1与S2有怎样的数量关系?并证明你的猜想.
分析 (1)根据旋转的性质可得AC=CD,然后求出△ACD是等边三角形,根据等边三角形的性质可得∠ACD=60°,然后根据内错角相等,两直线平行解答;
(2)过D点作DN⊥BC于N,AM⊥CE于M,先依据AAS求得△ACM≌△DCN求得AM=DN,然后根据等底等高的三角形面积相等.
解答 解:(1)DF∥AC;
∵∠ACB=90°,∠B=∠E=30°,
∴∠A=∠CDE=60°,
∵AC=DC,
∴△ACD是等边三角形,
∴∠ACD=60°=∠CDE,
∴DF∥AC,
∴∠CFD=90°,∠DCF=30°,
∴DF=$\frac{1}{2}$DC=$\frac{1}{2}$AC;
(2)S1=S2;
过D点作DN⊥BC于N,AM⊥CE于M,如图③,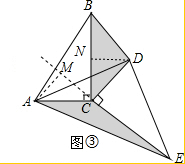
∵∠ECD=90°,
∴∠DCM=90°
∴∠DCN=90°-∠NCM,
又∵∠ACM=90°-∠NCM,
∴∠ACM=∠DCN,
在△ACM与△DCN中,
$\left\{\begin{array}{l}{∠ACM=∠DCN}\\{AC=CD}\\{∠AMC=∠DNC}\end{array}\right.$,
∴△ACM≌△DCN(AAS),
∴AM=DN,
又∵CE=BC,
∴$\frac{1}{2}$BC•DN=$\frac{1}{2}$CE•AM,
即S1=S2.
点评 本题考查了等边三角形的判定及性质平行线的判定及性质,全等三角形的判定及性质以及等底等高的三角形面积相等.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | (3x2)3=9x6 | B. | a6÷a2=a3 | C. | (a+b)2=a2+b2 | D. | (a-b)(a+b)=a2-b2 |
18.若反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,则k的取值可能是( )
| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
15.对于一次函数y=-x+2,下列结论错误的是( )
| A. | y随着x的增大而减小 | |
| B. | 函数图象不经过第三象限 | |
| C. | 函数图象向下平移2个单位长度得到y=-x的图象 | |
| D. | 函数图象与x轴的交点是(0,2) |
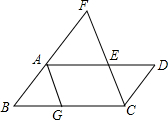 如图,点E是?ABCD的边AD上一点,连接CE并延长交BA的延长线于点F,若BG=DE,并且∠AEF=70°.求∠AGB的度数.
如图,点E是?ABCD的边AD上一点,连接CE并延长交BA的延长线于点F,若BG=DE,并且∠AEF=70°.求∠AGB的度数.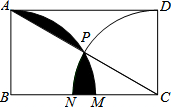 如图,在矩形ABCD中,AB=1,分别以点B、C为圆心,1为半径画弧,与BC边分别交于点M、N,且与对角线AC交于同一点P,则图中阴影部分的面积为$\frac{π}{3}$-$\frac{\sqrt{3}}{2}$.
如图,在矩形ABCD中,AB=1,分别以点B、C为圆心,1为半径画弧,与BC边分别交于点M、N,且与对角线AC交于同一点P,则图中阴影部分的面积为$\frac{π}{3}$-$\frac{\sqrt{3}}{2}$.