题目内容
11.某商场二楼摆出一台游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物,等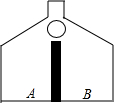 可能地向左或向右边落下.
可能地向左或向右边落下.(1)若乐乐投入一个小球,则小球落入B区域的概率为$\frac{1}{2}$.
(2)若乐乐先后投两个小球,求两个小球同时落在A区域的概率.
分析 (1)根据乐乐投入一个小球和概率公式直接得出答案;
(2)根据题意先画出树状图,得出等可能的情况数,再根据概率公式列式即可得解.
解答 解:(1)∵乐乐投入一个小球,
∴小球落入B区域的概率为$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)先后共投2个小球,可能会出现的结果列树状图如下: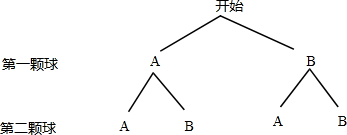
由树状图可知,共有4种等可能情况,其中2个小球均落在A区只有1种情况,
则2个小球均落在A区的概率为$\frac{1}{4}$.
点评 本题考查的是用列表法或画树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
2.-8的相反数是( )
| A. | 8 | B. | -$\frac{1}{8}$ | C. | $\frac{1}{8}$ | D. | -8 |
6.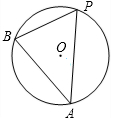 如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
 如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )
如图,⊙O为△ABP的外接圆,若⊙O的半径为2,∠P=75°,则$\widehat{AB}$的长为( )| A. | $\frac{5}{12}$π | B. | π | C. | $\frac{5}{3}$π | D. | 2π |

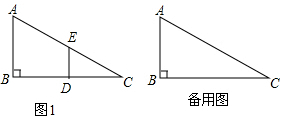 如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D、E分别是边BC、AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.