题目内容
1.化简(1)$\sqrt{8}$+$\sqrt{18}$;
(2)($\sqrt{6}$-2$\sqrt{3}$)×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$.
分析 (1)直接化简二次根式进而得出答案;
(2)直接利用二次根式乘法运算法则计算得出答案.
解答 解:(1)$\sqrt{8}$+$\sqrt{18}$
=2$\sqrt{2}$+3$\sqrt{2}$
=5$\sqrt{2}$;
(2)($\sqrt{6}$-2$\sqrt{3}$)×$\sqrt{3}$-6$\sqrt{\frac{1}{2}}$
=3$\sqrt{2}$-6-6×$\frac{\sqrt{2}}{2}$
=-6.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
16.某工艺厂计划一周生产工艺品2100个,要求每天生产300个,但实际每天生产量与计划相比有出入,如表是某周的生产情况(超产记为正、减产记为负):
(1)该厂星期一生产工艺品的数量为316个;
(2)本周产量中最多的一天比最少的一天多生产26个工艺品;
(3)求该工艺厂在本周实际生产工艺品多少个?
(4)已知该厂实际每日计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元,求该工艺厂在这一周应付出的工资总额是多少元?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 增减(单位:个) | +5 | -2 | -5 | +15 | -10 | +16 | -9 |
(2)本周产量中最多的一天比最少的一天多生产26个工艺品;
(3)求该工艺厂在本周实际生产工艺品多少个?
(4)已知该厂实际每日计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元,求该工艺厂在这一周应付出的工资总额是多少元?
6.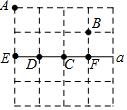 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
 如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )
如图的4×4的正方形网格中,有A、B两点,在直线a上求一点P,使PA+PB最短,则点P应选在( )| A. | C点 | B. | D点 | C. | E点 | D. | F点 |
 可能地向左或向右边落下.
可能地向左或向右边落下.
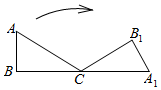 如图,在Rt△ABC中,∠A=60°,AB=1,将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置,点A1刚好落在BC的延长线上,求点A从开始到结束所经过的路径长为(结果保留π)$\frac{5}{3}$π.
如图,在Rt△ABC中,∠A=60°,AB=1,将Rt△ABC绕点C按顺时针方向旋转到△A1B1C的位置,点A1刚好落在BC的延长线上,求点A从开始到结束所经过的路径长为(结果保留π)$\frac{5}{3}$π.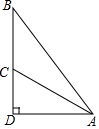 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,求旗杆BC的高度.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,求旗杆BC的高度.