题目内容
4．先化简，再求值：$\frac{x-3}{{x}^{2}-4}$÷（$\frac{1}{x}$-$\frac{1}{{x}^{2}-2x}$），其中x=$\sqrt{2}$-2．分析 先算括号里面的，再算除法，最后把x的值代入进行计算即可．
解答 解：原式=$\frac{x-3}{（x+2）（x-2）}$÷[$\frac{1}{x}$-$\frac{1}{x（x-2）}$]
=$\frac{x-3}{（x+2）（x-2）}$÷$\frac{x-2-1}{x（x-2）}$
=$\frac{x-3}{（x+2）（x-2）}$÷$\frac{x-3}{x（x-2）}$
=$\frac{x-3}{（x+2）（x-2）}$•$\frac{x（x-2）}{x-3}$
=$\frac{x}{x+2}$，
当x=$\sqrt{2}$-2时，原式=$\frac{\sqrt{2}-2}{\sqrt{2}-2+2}$=$\frac{\sqrt{2}-2}{\sqrt{2}}$=1-$\sqrt{2}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
14．
一个简单空间几何体的三视图如图所示，则这个几何体是（ ）
一个简单空间几何体的三视图如图所示，则这个几何体是（ ）| A． | 三棱锥 | B． | 四棱锥 | C． | 三棱柱 | D． | 四棱柱 |
15．下列各数中，无理数的是（ ）
| A． | $\frac{22}{7}$ | B． | ${（{\sqrt{5}}）^0}$ | C． | π | D． | $\sqrt{4}$ |
12．
如图所示的是一次函数y=kx+b（k≠0）的图象，则关于x的不等式k（x-1）+b＞0的解集为（ ）
如图所示的是一次函数y=kx+b（k≠0）的图象，则关于x的不等式k（x-1）+b＞0的解集为（ ）| A． | x＜3 | B． | x＞3 | C． | x＜4 | D． | x＞4 |
二次函数y=ax2+bx+c的图象如图所示，判断a，b，c，2a+b，a+b+c，a-b+c的符号．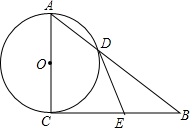
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，点E是BC的中点，连结DE．
如图，打台球时，选择适当的方向击打白球，白球反弹后击打红球，红球会直接入袋，此时，哪些角互为余角？哪些角互为补角？