题目内容
4.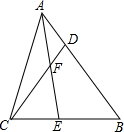 已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.
已知,如图,在△ABC中,AE是角平分线,D是AB上的点,AE、CD相交于点F.(1)若∠ACB=∠CDB=90°,求证:∠CFE=∠CEF;
(2)若∠ACB=∠CDB=m(0°<m<180°).
①求∠CEF-∠CFE的值(用含m的代数式表示);
②是否存在m,使∠CEF小于∠CFE,如果存在,求出m的范围,如果不存在,请说明理由.
分析 (1)先根据∠ACB=∠CDB=90°得出∠B=90°-∠DCB,∠ACD=90°-∠DCB,再由AE平分∠CAB即可得出结论;
(2)①根据三角形外角的性质可得出∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,故∠CFE-∠CEF=∠B-∠ACD,再由∠B=180°-m-∠DCB,∠ACD=m-∠DCB即可得出结论;
②根据∠CEF小于∠CFE可知∠CEF-∠CFE<0,故180°-2m<0,进而可得出结论.
解答 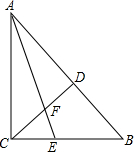 解:(1)∵∠ACB=∠CDB=90°,
解:(1)∵∠ACB=∠CDB=90°,
∴∠B=90°-∠DCB,∠ACD=90°-∠DCB,
∴∠B=∠ACD.
∵AE平分∠CAB,
∴∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,
∴∠CFE=∠CEF;
(2)①∵∠CFE=∠ACD+$\frac{1}{2}$∠CAB,∠CEF=∠B+$\frac{1}{2}$∠CAB,
∴∠CFE-∠CEF=∠B-∠ACD.
∵∠B=180°-m-∠DCB,∠ACD=m-∠DCB,
∴∠CEF-∠CFE=(180°-m-∠DCB)-(m-∠DCB)=180°-2m;
②存在.
∵要使∠CEF小于∠CFE,则∠CEF-∠CFE<0,
∴180°-2m<0,解得m>90°,
∴当90°<m<180°时,∠CEF的值小于∠CFE.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.张老师周末到某家居建材市场购买沙发、橱窗和地板三样物品,碰巧该市场推出“迎圣诞元旦双节”优惠活动,具体优惠情况如下:
(1)若购买三样物品原价8000元,请求出张老师实际的付款金额?
(2)若购买三样物品实际花费了6820元.
①请求出三件物品的原价总共是多少钱?
②几天后,张老师发现地板的样式不适合需要退货,该市场规定:消费者需支付优惠差额(即退货商品在购买时所享受的优惠),并且还要支付商品原价5%的手续费,最终该市场退还了张老师2345元,请问地板原价是多少钱?
| 购物总金额(原价) | 优惠率 |
| 不超过5000元的部分 | 10% |
| 超过5000元且不超过10000元的部分 | 20% |
| 超过10000元且不超过20000元的部分 | 30% |
| … | … |
(2)若购买三样物品实际花费了6820元.
①请求出三件物品的原价总共是多少钱?
②几天后,张老师发现地板的样式不适合需要退货,该市场规定:消费者需支付优惠差额(即退货商品在购买时所享受的优惠),并且还要支付商品原价5%的手续费,最终该市场退还了张老师2345元,请问地板原价是多少钱?
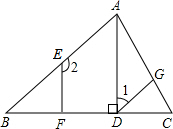 如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数.
如图,已知AD是△ABC的高,点E、G分别在AB、AC上,EF⊥BC,垂足为F,∠CGD=∠BAC,若∠1=50°,求∠2和∠B的度数. 如图,已知∠1=∠2,∠3=50°,求∠4的大小.
如图,已知∠1=∠2,∠3=50°,求∠4的大小. 在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.
在△ABC中,∠ABC=∠ACB=2∠A,BD是∠ABC的平分线,交AB边上的高CE于点H,求∠BHC的度数.