��Ŀ����
14������ѧ��������кܶ���۵���ʽ��ͳһ�ģ���Ҳ��������ѧ����������֤���������������У����е�ʽ$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{3}}$��������1����ͼ1����APC=120�㣬PBƽ�֡�APC��ֱ��l��PA��PB��PC�ֱ��ڵ�A��B��C��PA=x1��PC=x2��PB=x3��
��2����ͼ2����ƽ��ֱ������ϵxOy�У�����A��x1��0����B��0��x2����ֱ��l����ֱ��y=x���ڵ�C����C������Ϊx3��
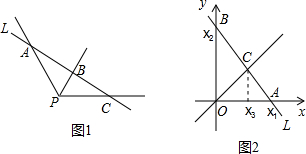
���� ��1����ͼ1�У�����B��BE��PA��PC�ڵ�E����BE��PA���Ƴ���BEC�ס�APC���õ�$\frac{BE}{AP}$=$\frac{EC}{PC}$����$\frac{{x}_{3}}{{x}_{1}}$=$\frac{{x}_{2}-{x}_{3}}{{x}_{2}}$����x2x3+x1x3=x1x2�����߳���x1x2x3���ɽ�����⣮
��2����ͼ2�У�����C��CD��x���ڵ�D��CE��y���ڵ�E����S��BOC+S��AOC=S��AOB���г�ʽ�ӣ����ɽ�����⣮
��� ��1��֤������ͼ1�У�����B��BE��PA��PC�ڵ�E��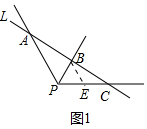
��BE��PA��
���BEC�ס�APC��
�ߡ�APC=120�㣬PBƽ�֡�APC���ɵá�PBE�ǵȱ������Σ�
��BE=PE=PB=x3��
��EC=x2-x3��
��$\frac{BE}{AP}$=$\frac{EC}{PC}$��
��$\frac{{x}_{3}}{{x}_{1}}$=$\frac{{x}_{2}-{x}_{3}}{{x}_{2}}$��
��x2x3+x1x3=x1x2��
��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{3}}$��
�ڽ⣺��ͼ2�У�����C��CD��x���ڵ�D��CE��y���ڵ�E��
�ߵ�C��ֱ��y=x�ϣ��Һ�����Ϊx3�����C��x3��x3����
��CE=CD=x3��
��S��BOC+S��AOC=S��AOB��
��$\frac{1}{2}$x2x3+$\frac{1}{2}$x1x3=$\frac{1}{2}$x1x2��
��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{1}{{x}_{3}}$��
���� ���⿼��һ�κ����ۺ��⡢���������ε��ж������ʡ������ε������֪ʶ������Ĺؼ������Ӧ����ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ��������������ν�����⣬�����п�ѹ���⣮

 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д�| ����ˮ���ۼ۸� | ��ˮ�����۸� | |
| ÿ��ÿ����ˮ�� | ���ۣ�Ԫ/�� | ���ۣ�Ԫ/�� |
| 17�ּ����� | a | 0.80 |
| ����17�ֵ�������30�ֵIJ��� | b | 0.80 |
| ����30�ֵIJ��� | 6.00 | 0.80 |
��֪С����2015��5�·���ˮ20�֣���ˮ��66Ԫ��6�·���ˮ25�֣���ˮ��91Ԫ��
��1����a��b��ֵ��
��2����������ĵ�������ˮ�������ӣ�Ϊ�˽�ʡ��֧��С���ƻ���7�·�ˮ�ѿ����ڲ�������ͥ�������2%����С���ҵ�������Ϊ9600Ԫ����С����7�·��������ˮ���ٶ֣��������ȷ��1�֣�
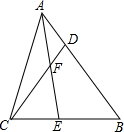 ��֪����ͼ���ڡ�ABC�У�AE�ǽ�ƽ���ߣ�D��AB�ϵĵ㣬AE��CD�ཻ�ڵ�F��
��֪����ͼ���ڡ�ABC�У�AE�ǽ�ƽ���ߣ�D��AB�ϵĵ㣬AE��CD�ཻ�ڵ�F��
 ��֪����ͼ��OD��AD��OH��AE��DE��GH��O��
��֪����ͼ��OD��AD��OH��AE��DE��GH��O��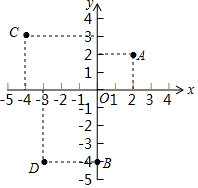 д����ͼ��ʾ��ƽ��ֱ������ϵ��A��B��C��D������꣬���ֱ�ָ���������ڵ����ޣ�
д����ͼ��ʾ��ƽ��ֱ������ϵ��A��B��C��D������꣬���ֱ�ָ���������ڵ����ޣ�