题目内容
7.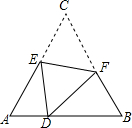 如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
分析 借助翻折变换的性质得到DE=CE;设AB=3k,CE=x,则AE=3k-x;根据相似三角形的判定与性质即可解决问题.
解答 解:设AD=k,则DB=2k,
∵△ABC为等边三角形,
∴AB=AC=3k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,
∴$\frac{ED}{FD}=\frac{AD}{BF}=\frac{AE}{BD}$,
设CE=x,则ED=x,AE=3k-x,
设CF=y,则DF=y,FB=3k-y,
∴$\frac{x}{y}=\frac{k}{3k-y}=\frac{3k-x}{2k}$,
∴$\left\{\begin{array}{l}{ky=x(3k-y)}\\{2kx=y(3k-x)}\end{array}\right.$,
∴$\frac{x}{y}$=$\frac{4}{5}$,
∴CE:CF=4:5.
故选:B.
解法二:解:设AD=k,则DB=2k,
∵△ABC为等边三角形,
∴AB=AC=3k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,由折叠,得
CE=DE,CF=DF
∴△AED的周长为4k,△BDF的周长为5k,
∴△AED与△BDF的相似比为4:5
∴CE:CF=DE:DF=4:5.
故选:B.
点评 主要考查了翻折变换的性质及其应用问题;解题的关键是借助相似三角形的判定与性质(用含有k的代数式表示);对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
18.如图,有一块矩形纸片ABCD,AB=8,AD=6,将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则△CEF的面积为( )
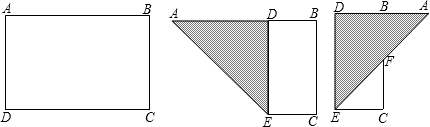

| A. | $\frac{1}{2}$ | B. | $\frac{9}{8}$ | C. | 2 | D. | 4 |
15.在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
| A. | (3,2) | B. | (2,-3) | C. | (-3,-2) | D. | (3,-2) |
12. 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
16.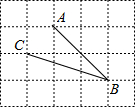 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
 如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )
如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( )| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{1}{2}$ |
 如图,已知锐角△ABC.
如图,已知锐角△ABC.