题目内容
16．
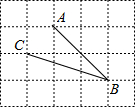如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是（ ）| A． | 2 | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{\sqrt{5}}{5}$ | D． | $\frac{1}{2}$ |
分析 根据勾股定理，可得AC、AB的长，根据正切函数的定义，可得答案．
解答 解：如图：
，
由勾股定理，得
AC=$\sqrt{2}$，AB=2$\sqrt{2}$，BC=$\sqrt{10}$，
∴△ABC为直角三角形，
∴tan∠B=$\frac{AC}{AB}$=$\frac{1}{2}$，
故选：D．
点评 本题考查了锐角三角函数的定义，先求出AC、AB的长，再求正切函数．
练习册系列答案
阅读快车系列答案
相关题目
7．
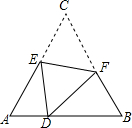如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（ ）
如图，D是等边△ABC边AB上的一点，且AD：DB=1：2，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF=（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{6}$ | D． | $\frac{6}{7}$ |
4．
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（ ）
如图，将一块含有30°角的直角三角板的两个顶点放在矩形直尺的一组对边上．如果∠2=60°，那么∠1的度数为（ ）| A． | 60° | B． | 50° | C． | 40° | D． | 30° |
如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m2？
如图，△ABC是直角三角形，∠ACB=90°．
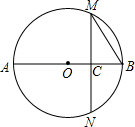如图，圆O的直径AB=8，AC=3CB，过C作AB的垂线交圆O于M，N两点，连结MB，则∠MBA的余弦值为$\frac{1}{2}$．
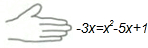老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了如图所示的一个二次三项式，形式如图：
6．下列说法正确的是（ ）
| A． | “购买1张彩票就中奖”是不可能事件 | |
| B． | “掷一次骰子，向上一面的点数是6”是随机事件 | |
| C． | 了解我国青年人喜欢的电视节目应作全面调查 | |
| D． | 甲、乙两组数据，若S甲2＞S乙2，则乙组数据波动大 |