题目内容
17.已知点A(-2,n)在抛物线y=x2+bx+c上.(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
分析 (1)代入b=1,c=3,以及A点的坐标即可求得n的值;
(2)根据题意求得抛物线的解析式为y=(x-1)2-4,从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x′2-4,然后利用5点式画出函数的图象即可.
解答 解:(1)∵b=1,c=3,A(-2,n)在抛物线y=x2+bx+c上.
∴n=4+(-2)×1+3=5.
(2)∵此抛物线经过点A(-2,n),B(4,n),
∴抛物线的对称轴x=$\frac{-2+4}{2}$=1,
∵二次函数y=x2+bx+c的最小值是-4,
∴抛物线的解析式为y=(x-1)2-4,
令x-1=x′,
∴点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x′2-4,
点P(x-1,x2+bx+c)的纵坐标随横坐标变化的如图: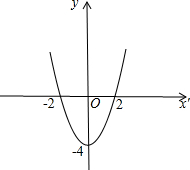
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征以及二次函数的最值等,根据题意求得抛物线的解析式是解题的关键.

练习册系列答案
相关题目
7.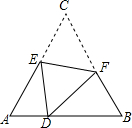 如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
 如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )
如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | $\frac{6}{7}$ |
12.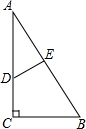 如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
 如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )
如图,在△ABC中,∠C=90°,点D,E分别在边AC,AB上.若∠B=∠ADE,则下列结论正确的是( )| A. | ∠A和∠B互为补角 | B. | ∠B和∠ADE互为补角 | ||
| C. | ∠A和∠ADE互为余角 | D. | ∠AED和∠DEB互为余角 |
9.设x1,x2是一元二次方程x2-2x-3=0的两根,则x12+x22=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
6.下列说法正确的是( )
| A. | “购买1张彩票就中奖”是不可能事件 | |
| B. | “掷一次骰子,向上一面的点数是6”是随机事件 | |
| C. | 了解我国青年人喜欢的电视节目应作全面调查 | |
| D. | 甲、乙两组数据,若S甲2>S乙2,则乙组数据波动大 |
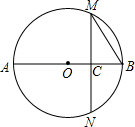 如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为$\frac{1}{2}$.
如图,圆O的直径AB=8,AC=3CB,过C作AB的垂线交圆O于M,N两点,连结MB,则∠MBA的余弦值为$\frac{1}{2}$.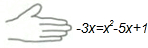 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图:
老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了如图所示的一个二次三项式,形式如图: