题目内容
2.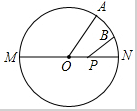 如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.
如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.
分析 作点B关于MN的对称点B′,交MN于点P,连接OB′.先求得∠AOB′=90°,由轴对称的性质可知PB=PB′,故此PA+PB=PA+PB′,当点A、P、B′在一条直线时,PA+PB有最小值,然后在Rt△AB′O中,利用勾股定理可求得AB′的长.
解答 解:作点B关于MN的对称点B′,交MN于点P,连接OB′.
∵$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,
∴劣弧NB=30°.
∵点B′与点B关于MN对称,
∴劣弧NB′=30°,PB=PB′.
∴∠AOB′=90°,PA+PB=PA+PB′=AB.
∵MN是圆O的直径,
∴OA=OB′=$\frac{1}{2}MN$=1.
在Rt△AOB′中,AB′=$\sqrt{O{A}^{2}+OB{′}^{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查的是圆的性质、勾股定理的应用、轴对称的性质,明确当点A、P、B′在一条直线时,PA+PB有最小值是解题的关键.

练习册系列答案
相关题目
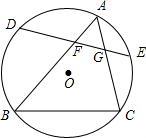 如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.
如图,△ABC三个顶点都在⊙O上,D,E分别为$\widehat{AB}$,$\widehat{AC}$中点,弦DE交AB于点F,交AC于点G,求证:AF•AG=DF•EG.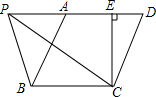 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;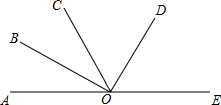 如图所示,O是直线AE上的-点,OB是∠AOC的平分线,OD是∠COE的平分线.
如图所示,O是直线AE上的-点,OB是∠AOC的平分线,OD是∠COE的平分线.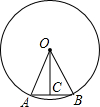 如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).
如图,⊙O的半径为20,$\widehat{AB}$的度数为36°,求弦AB及其弦心距OC的长(精确到0.1).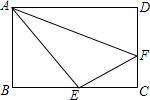 如图,在矩形ABCD中,点E为BC的中点,点F在CD上,要使△AEF的周长最小时,确定点F的位置的方法为作点E关于DC的对称点E′,连接AE′交CD于点F.
如图,在矩形ABCD中,点E为BC的中点,点F在CD上,要使△AEF的周长最小时,确定点F的位置的方法为作点E关于DC的对称点E′,连接AE′交CD于点F. 如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.
如图,在一块长为60m,宽40m的矩形荒地正中央挖一块与荒地长度比例相同的矩形水池,要使水池面积是原荒地面积的$\frac{1}{4}$,上下荒地等宽,左右荒地等宽,求四周剩余荒地的宽度.