题目内容
7．
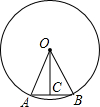如图，⊙O的半径为20，$\widehat{AB}$的度数为36°，求弦AB及其弦心距OC的长（精确到0.1）．
分析 根据垂径定理得到AC=BC，根据等腰三角形的性质可以得到∠OAC=72°°，解直角三角形求得弦AB及其弦心距OC的长．
解答 解：如图，∵OC⊥AB，
∴AC=CB．
∵OA=OB，
∴△OAB为等腰三角形，
∵$\widehat{AB}$的度数为36°，
∴顶角∠AOB=36°，
∴底角∠OAC=72°，
∴AC=OA•cos72°=20×0.31≈6.2，OC=OA•sin72°=20×0.95≈19.0．
∴AB=2AC=12.4；
点评 本题考查的是垂径定理，等腰三角形的性质以及解直角三角形等，熟练掌握性质定理是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
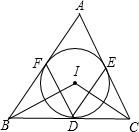已知⊙I为△ABC的内切圆，点D，E，F是切点，连接BI，CI，DE，DF，试猜想∠BIC与∠FDE有何数量关系，并证明你的猜想．
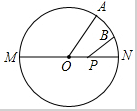如图，MN是⊙0的直径，MN=2，点A在⊙0上，$\widehat{AON}$=60°，点B为$\widehat{AON}$的中点，点P是直径MN上的一个动点，则PA+PB的最小值为$\sqrt{2}$．
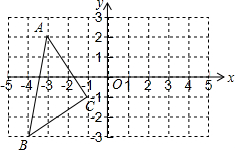如图，根据要求回答下列问题：
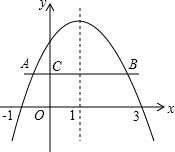已知二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=1，点A、B是二次函数图象上的两点，AB∥x轴且与y轴交于点C（点C在二次函数图象于y轴交点的下方），有下列结论：①ac＜0；②方程ax2+bx+c=0的两根是x1=-1，x2=3；③函数有最小值，最小值是a+b+c；④当x＞0时，y随x的增大而减小；⑤BC=3AC．其中正确的结论的序号是①、②．
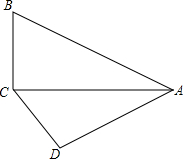如图，在△ABC与△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD=30°，则$\frac{{S}_{△ABC}}{{S}_{△ACD}}$=$\frac{4}{3}$．