题目内容
13．
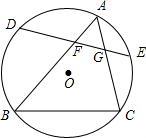如图，△ABC三个顶点都在⊙O上，D，E分别为$\widehat{AB}$，$\widehat{AC}$中点，弦DE交AB于点F，交AC于点G，求证：AF•AG=DF•EG．
分析 根据相似三角形的判定定理证得△ADF∽△EAG，然后由相似三角形的对应边成比例求得$\frac{AF}{EG}=\frac{DF}{AG}$，即AF•AG=DF•EG．
解答 
证明：如图，连接AD，AE，
∵D、E分别是AB、AC的中点，
∴AD=BD，AE=CE，
∴∠BAD=∠E，（等弧所对的圆周角相等）
∠CAE=∠D，
∴△ADF∽△EAG
∴$\frac{AF}{EG}=\frac{DF}{AG}$，
∴AF•AG=DF•EG．
点评 本题考查了相似三角形的判定与性质、圆周角定理．在证明△ADF∽△EAG时，利用等弧所对的弦相等证明AD=BD，AE=CE是关键．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
4．点A（-3，2）关于x轴的对称点A′的坐标为（ ）
| A． | （-3，-2） | B． | （3，2） | C． | （3，-2） | D． | （2，-3） |
8．
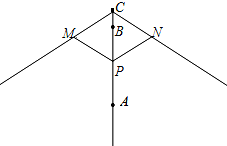如图为太阳伞示意图，当伞收紧时，点P与点A重合，当伞慢慢撑开时，动点P由A向B移动；当点P到过点B时，伞张得最开．已知伞在撑开的过程中，总有PM=PN=CM=CN．则下列说法错误的是（ ）
如图为太阳伞示意图，当伞收紧时，点P与点A重合，当伞慢慢撑开时，动点P由A向B移动；当点P到过点B时，伞张得最开．已知伞在撑开的过程中，总有PM=PN=CM=CN．则下列说法错误的是（ ）| A． | 四边形PNCM可能会出现为正方形 | B． | 四边形PNCM的周长始终不变 | ||
| C． | 当∠CPN=60°时，CP=AP | D． | 四边形PNCM的面积始终不变 |
如图，一只虫子从圆柱上A点处，绕圆柱一圈爬到B处，你能画出它爬行的最短路线吗？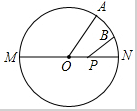
如图，MN是⊙0的直径，MN=2，点A在⊙0上，$\widehat{AON}$=60°，点B为$\widehat{AON}$的中点，点P是直径MN上的一个动点，则PA+PB的最小值为$\sqrt{2}$．
如图，已知△ABC中，AB＞AC．求证：∠C＞∠B．