题目内容
10.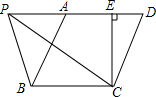 如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;
如图,?ABCD中,BC=5cm,CD=6cm,CE⊥AD于点E,CE=4cm,P为直线AD上一点.求;(1)△PBC的面积;
(2)AB与CD之间的距离.
分析 (1)根据平行四边形ABCD的性质得到AD∥BC,则直线AD与直线BC间的距离处处相等,即△PBC的边BC上的高线即为CE的长度,由三角形的面积公式可以求得答案;
(2)利用面积法来求AB与CD之间的距离.
解答  解:(1)如图,∵四边形ABCD是平行四边形,
解:(1)如图,∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵BC=5cm,CE⊥AD于点E,CE=4cm,
∴S△PBC=$\frac{1}{2}$BC•CE=$\frac{1}{2}$×5×4=10(cm2);
(2)设AB与CD之间的距离为h,则
CD•h=BC•CE,即6h=5×4,
则h=$\frac{10}{3}$.
即AB与CD之间的距离是$\frac{10}{3}$cm.
点评 本题考查了平行四边形的性质.解题时,利用了平行四边形的对边相互平行和平行线间的距离处处相等的性质.

练习册系列答案
相关题目
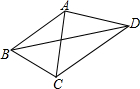 如图,已知AB=AC=AD,∠CBD=2∠BDA,∠BAC=48°.
如图,已知AB=AC=AD,∠CBD=2∠BDA,∠BAC=48°. 如图,一只虫子从圆柱上A点处,绕圆柱一圈爬到B处,你能画出它爬行的最短路线吗?
如图,一只虫子从圆柱上A点处,绕圆柱一圈爬到B处,你能画出它爬行的最短路线吗?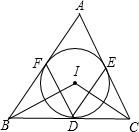 已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想.
已知⊙I为△ABC的内切圆,点D,E,F是切点,连接BI,CI,DE,DF,试猜想∠BIC与∠FDE有何数量关系,并证明你的猜想.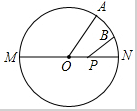 如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.
如图,MN是⊙0的直径,MN=2,点A在⊙0上,$\widehat{AON}$=60°,点B为$\widehat{AON}$的中点,点P是直径MN上的一个动点,则PA+PB的最小值为$\sqrt{2}$.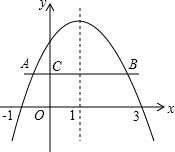 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,点A、B是二次函数图象上的两点,AB∥x轴且与y轴交于点C(点C在二次函数图象于y轴交点的下方),有下列结论:①ac<0;②方程ax2+bx+c=0的两根是x1=-1,x2=3;③函数有最小值,最小值是a+b+c;④当x>0时,y随x的增大而减小;⑤BC=3AC.其中正确的结论的序号是①、②.
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,点A、B是二次函数图象上的两点,AB∥x轴且与y轴交于点C(点C在二次函数图象于y轴交点的下方),有下列结论:①ac<0;②方程ax2+bx+c=0的两根是x1=-1,x2=3;③函数有最小值,最小值是a+b+c;④当x>0时,y随x的增大而减小;⑤BC=3AC.其中正确的结论的序号是①、②.