题目内容
14.已知a=$\frac{1}{\sqrt{2}+1}$,求$\frac{2}{a}$-$\frac{\sqrt{{a}^{2}-2a+1}}{{a}^{2}-a}$的值?分析 首先把a化简,把所求的式子进行化简,然后代入求值即可.
解答 解:a=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1,
则原式=2×$\frac{1}{a}$-$\frac{|a-1|}{a(a-1)}$=2($\sqrt{2}$-1)-$\frac{2-\sqrt{2}}{(\sqrt{2}-1)(\sqrt{2}-2)}$=2$\sqrt{2}$-2+$\frac{1}{\sqrt{2}-1}$=2$\sqrt{2}$-2+$\sqrt{2}$+1=3$\sqrt{2}$-1.
点评 本题考查了二次根式的化简求值,正确把二次根式进行化简是关键.

练习册系列答案
相关题目
5.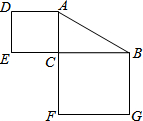 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
 如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )
如图,在Rt△ABC中,∠C=90°,若AB=15,则正方形ADEC和正方形BCFG的面积和为( )| A. | 225 | B. | 200 | C. | 250 | D. | 150 |
19. 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )
 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )| A. | CD垂直平分AD | B. | AB垂直平分CD | C. | CD平分∠ACB | D. | 以上结论均不对 |
6.在计算结果为a6的个数是( )
| A. | a2•a3 | B. | a12÷a2 | C. | (-a2)3 | D. | a4•a2 |
3.下列二次根式中是最简二次根式的是( )
| A. | $\sqrt{4x}$ | B. | $\sqrt{\frac{1}{x}}$ | C. | $\sqrt{{x}^{2}+{y}^{2}-2xy}$ | D. | $\sqrt{{x}^{2}-{y}^{2}}$ |
 如图,矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长是4.
如图,矩形ABCD两条对角线相交于点O,∠AOD=120°,AB=2,则矩形的对角线AC的长是4.