题目内容
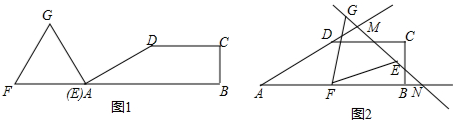
1.如图①,在梯形ABCD中,AB∥CD,∠B=90°,AB=6,CD=3,BC=$\sqrt{3}$.△EFG是边长为3的等边三角形,且与梯形ABCD位于直线AB同侧,点E与点A重合,EF与AB在同一直线上.△EFG以每秒1个单位的速度沿直线AB向右平移,当点E与点B重合时运动停止.设△EFG的运动时间为t(秒).(1)当△EFG的边EG经过点D时,求t的值;
(2)在平移过程中,设△EFG与梯形ABCD重叠部分的面积为S,请直接写出S与t的函数关系式及其对应的自变量t的取值范围;
(3)如图②,当△EFG的平移运动停止后(此时点B与点E重合),将△EFG绕点F进行旋转,在旋转过程中,设EG所在直线与射线AD相交于点M,与射线FB相交于点N,当△AMN为等腰三角形时,求AN的长度.
分析 (1)过点D作DG⊥AB于点,构造矩形和直角三角形,求出AH,利用三角函数求出∠A=30°,由△EFG是边长为3的等边三角形,得到∠ADE=90°,∠EDH=30°
,运用三角函数求出HE,进而得到AE,求出t的值;
(2)分四段:当0≤t<3时;当3≤t<4时;当4≤t<5时;当5≤t≤6时;进行分别计算即可;
(3)分类讨论:当AM=MN时;当AM=AN时;当AN=MN时.
解答 解:(1)当EG经过点D时,如图1所示,过点D作DG⊥AB于
则在矩形BCDH中,BC=DH=$\sqrt{3}$,CD=BH=3,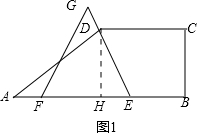
∵AB=6,
∴AH=3,
∴tanA=$\frac{DH}{AH}=\frac{\sqrt{3}}{3}$
∴∠A=30°
∵△EFG是边长为3的等边三角形,
∴∠GEF=∠GFE=∠G=60°,EF=EG=FG=3,
∴∠ADE=90°,∠EDH=30°,
∴HE=tan30°×DH=1,
∴AE=AH+HE=3+1=4
即t=4;
(2)①如图2所示,当0≤t<3时,AE=t,HE=$\frac{t}{2}$,AH=$\frac{\sqrt{3}}{2}$t
∴S=S△AHE=$\frac{1}{2}$•AH•HE=$\frac{1}{2}$×$\frac{t}{2}$×$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{8}$t2,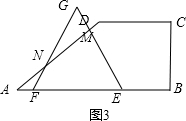
②如图3所示,当3≤t<4时,AE=t,DE=$\frac{t}{2}$,MG=3-$\frac{t}{2}$;
∴MN=$\sqrt{3}$MG=3$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t,
∴S=S△GEF-S△MGN
=$\frac{1}{2}$EF2•cos30°-$\frac{1}{2}$•MN•MG
=-$\frac{\sqrt{3}}{8}{t}^{2}+\frac{\sqrt{3}}{2}t+\frac{7\sqrt{3}}{4}$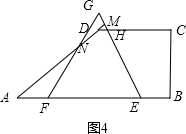
③如图4所示,当4≤t<5时,GH=1,ME=$\frac{t}{2}$,MG=3-$\frac{t}{2}$,MH=$\frac{t}{2}$-2,MN=$\sqrt{3}$MG,DH=$\sqrt{3}$MN,
∴S=S△GEF-S△MGN-S△DMH
=$\frac{1}{2}$EF2•cos30°-$\frac{1}{2}$•MN•MG-$\frac{1}{2}$•DH•MN
=-$\frac{\sqrt{3}}{8}{t}^{2}+\frac{\sqrt{3}}{2}t+\frac{7\sqrt{3}}{4}$-$\frac{\sqrt{3}}{2}$($\frac{t}{2}$-2)2
=-$\frac{\sqrt{3}}{4}{t}^{2}-\frac{5\sqrt{3}}{2}t-\frac{17\sqrt{3}}{4}$;
④如图5所示,当5≤t≤6时,MN=1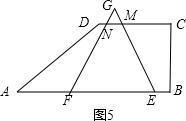
∴S=S△GEF-S△MGN
=$\frac{9\sqrt{3}}{4}-\frac{\sqrt{3}}{4}$
=2$\sqrt{3}$;
综上所述:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{8}{t}^{2}(0≤t<3)}\\{-\frac{\sqrt{3}}{8}{t}^{2}+\frac{3\sqrt{3}}{2}t-\frac{9\sqrt{3}}{4}(3≤t<4)}\\{-\frac{\sqrt{3}}{4}{t}^{2}+\frac{5\sqrt{3}}{2}t-\frac{17\sqrt{3}}{4}(4≤t<5)}\\{2\sqrt{3}(5≤t≤6)}\end{array}\right.$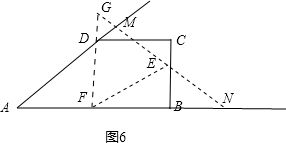
(3)如图6所示,当AM=MN时,则∠N=∠A=30°,
∵∠G=60°,
∴GF⊥AN,
∴FN=3$\sqrt{3}$,
∴AN=AF+FN=3+3$\sqrt{3}$
如图7所示,当AM=AN时,过点G作GP⊥AB交EF于点Q,
∵∠A=30°,
∴∠MNA=75°,
∴∠GFN=75°,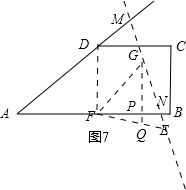
∵∠FGN=60°,
∴∠FGP=180°-75°-60°=45°,
∴△PFG为等腰直角三角形,
易证△EFN≌△EGQ,
∴△PQF≌△PNG,
∵△ENQ为等边三角形,FG=3
∴PF=GP=$\frac{3\sqrt{2}}{2}$
设PN=x,则NE=NQ=$\sqrt{2}$x
在Rt△PNG中,NG=3-x,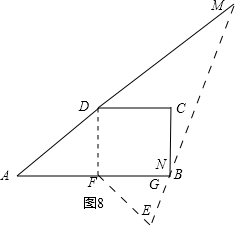
∴(3-$\sqrt{2}$x)2-x2=($\frac{3\sqrt{2}}{2}$)2,
解得:x=3$\sqrt{2}$-$\sqrt{6}$,
∴AN=AF+PF+PN=3+$\frac{3\sqrt{2}}{2}$+3$\sqrt{2}$-$\sqrt{6}$=3+$\frac{9\sqrt{2}}{2}-\sqrt{6}$;
如图8所示,当AN=MN时,显然此时G、N与点B重合,所以,AN=AB=6.
点评 本题需要用动态的角度来思考问题,做题时要认真分析问题,根据问题有目的性的找出已知条件,回答问题,第二小题要先确定自变量的t的取值范围,注意分段求出S与t的关系,第三小题等腰三角形存在性问题一定要分类讨论.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案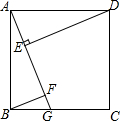 已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.
已知:在正方形ABCD中,点G是BC边上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.求证:AF=BF+EF.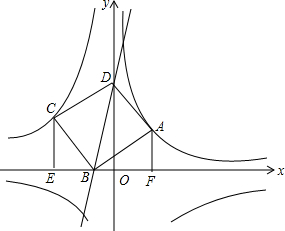 如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.
如图,点A(2,2)在双曲线y1=$\frac{k}{x}$(x>0)上,点C在双曲线y2=-$\frac{9}{x}$(x<0)上,分别过A、C向x轴作垂线,垂足分别为F、E,以A、C为顶点作正方形ABCD,且使点B在x轴上,点D在y轴的正半轴上.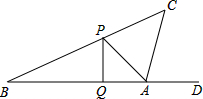 2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
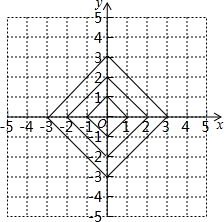 在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( )
在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,观察如图所示中每一个正方形(实践)四条边上的整点的个数,请你猜测由里向外第7个正方形(实线)四条边上的整点个数有( ) 如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距.
如图,AB是⊙O的直径,弦CD和AB相交于P,且∠APC=45°,OQ是弦CD的弦心距.