题目内容
19. 如图,AC=AD,BC=BD,则( )
如图,AC=AD,BC=BD,则( )| A. | CD垂直平分AD | B. | AB垂直平分CD | C. | CD平分∠ACB | D. | 以上结论均不对 |
分析 先根据全等三角形的判定定理得出△ABC≌△ABD,故可得出∠BAC=∠BAD,再由AC=AD即可得出结论.
解答 解:在△ABC与△ABD中,
∵$\left\{\begin{array}{l}AC=AD\\ BC=BD\\ AB=AB\end{array}\right.$,
∴△ABC≌△ABD,
∴∠BAC=∠BAD,即AB是∠CAD的平分线.
∵AC=AD,
∴AB是CD的垂直平分线.
故选B.
点评 本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
9.若x2-mx+4是完全平方式,则m=( )
| A. | 8 | B. | ±8 | C. | 4 | D. | ±4 |
7.下列运算正确的正确的是( )
| A. | $\sqrt{2m}$+$\sqrt{3m}$=$\sqrt{5m}$ | B. | 5$\sqrt{5}$-$\sqrt{5}$=4 | C. | 5+$\sqrt{2}$=5$\sqrt{2}$ | D. | m$\sqrt{x}$-n$\sqrt{x}$=(m-n)$\sqrt{x}$ |
4.⊙O1的半径为3厘米,⊙O2的半径为2厘米,圆心距O1O2=4厘米,这两圆的位置关系是( )
| A. | 内含 | B. | 内切 | C. | 相交 | D. | 外切 |
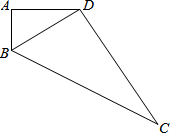 已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.
已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.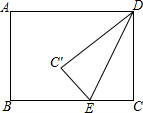 如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.
如图,矩形ABCD中,AB=6,BC=8,点E是射线CB上的一个动点,把△DCE沿DE折叠,点C的对应点为C′.