题目内容
9.已知a2-3a+1=0,求a2+$\frac{1}{{a}^{2}}$和a4+$\frac{1}{{a}^{4}}$的值.分析 在原方程的两边同时除以a,得到a-$\frac{1}{a}$=-4.利用完全平方公式的变形得到${a}^{2}+\frac{1}{{a}^{2}}$,利用完全平方公式的变形来求${a}^{4}+\frac{1}{{a}^{4}}$的值.
解答 解:a2-3a+1=0
在原方程的两边同时除以a,得:
a-3+$\frac{1}{a}$=0,
a+$\frac{1}{a}$=3,
$(a+\frac{1}{a})^{2}={3}^{2}$
${a}^{2}+2+\frac{1}{{a}^{2}}=9$
${a}^{2}+\frac{1}{{a}^{2}}$=7.
$({a}^{2}+\frac{1}{{a}^{2}})^{2}={7}^{2}$
${a}^{4}+2+\frac{1}{{a}^{4}}=49$
${a}^{4}+\frac{1}{{a}^{4}}=47$.
点评 本题既考查了对因式分解方法的掌握,又考查了代数式求值的方法,同时还隐含了整体的数学思想和正确运算的能力,解决本题的关键是熟记完全平分公式.

练习册系列答案
相关题目
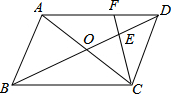 如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.
如图,平行四边形ABCD中,对角线AC,BD相交于O,BC=18,E为OD中点,连结CE并延长交AD于F,则DF=8.