题目内容
14.已知抛物线y=x2+bx+c与x轴只有一个公共点为A(2,0),求抛物线与y轴的交点B的坐标.分析 抛物线与x轴只有一个公共点,即点A为抛物线的顶点,从而可知对称轴为x=2,根据对称轴x=-$\frac{b}{2a}$即可求出b的值,将点A代入后即可求出c的值,从而可求出B的坐标.
解答 解:由题意可知:点A为抛物线的顶点,
∴-$\frac{b}{2}$=2
∴b=-4,
∴y=x2-4x+c
把(2,0)代入y=x2-4x+c,
∴c=4,
∴y=x2-4x+4,
令x=0代入y=x2-4x+4,
y=4,
∴B(0,4)
点评 本题考查抛物线与x轴的交点,解题的关键是根据A点的坐标求出b、c的值,本题属于基础题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.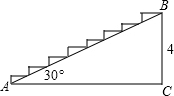 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
 现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)
现要把如图所示的楼梯铺上地毯,则所需地毯的长度约为( )(结果精确到0.1m)| A. | 6.9m | B. | 4m | C. | 8m | D. | 10.9m |
2.下列事件是随机事件的是( )
| A. | 两个整数相加,和是整数 | B. | 两个整数相减,差是整数 | ||
| C. | 两个整数相乘,积是整数 | D. | 两个整数相除,商是整数 |
6.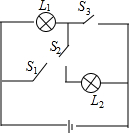 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
 如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )
如图所示电路,任意闭合两个开关,能使灯L2亮起来的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{5}$ |
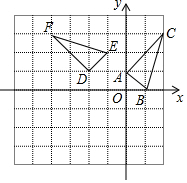 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0).
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是(-1,0).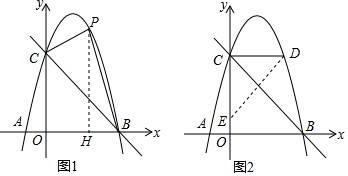
 如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.
如图,一段抛物线:y=2x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…,如此进行下去,直至的C10,(1)请写出抛物线C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段抛物线C10上,则m=-260.