题目内容
19.如图,抛物线y=ax2+bx-4a经过A(-1,0),C(0.4)两点,与x轴交于另一点B.(1)求抛物线的解析式;
(2)点P为抛物线第一象限上的点,求四边形PBOC的最大面积;
(3)已知点D(m,m+1)在第一象限的抛物线上,求点D关于直线BC对称的点的坐标.
分析 (1)直接将点A(-1,0),C(0.4)两点代入抛物线解析式y=ax2+bx-4a,解得a,b,可得结果;
(2)由(1)的结果,可设点P的坐标是(x,-x2+3x+4)解得点B的坐标,利用梯形和三角形的面积公式可得四边形PBOC的面积,利用二次函数的最值可得最大面积;
(3)由点D(m,m+1)在第一象限的抛物线上可得m的值,易得点D的坐标,可得∠OBC=45°,易得CD∥AB且CD=3,设点D关于直线BC的对称点为点E,可得点E在y轴上,且CE=CD=3,易得点E的坐标,即得结果.
解答 解:(1)∵抛物线y=ax2+bx-4a经过C(0.4),
∴-4a=4,
a=-1,
将A(-1,0)代入y=-x2+bx+4,得
-1-b+4=0,
∴b=3.
∴抛物线的解析式为y=-x2+3x+4;
(2)由已知,可设点P的坐标是(x,-x2+3x+4)
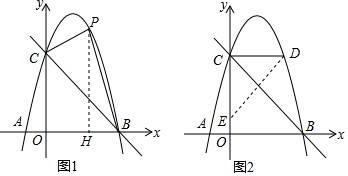
如图1,作PH⊥x轴于H,则OH=x,PH=-x2+3x+4,
由(1),当-x2+3x+4=0时,解得x=-1或x=4,
∴点B的坐标是(4,0),∴OB=4;
∵点C的坐标是(0,4),∴OC=4.
∴S四边形PBOC=S四边形PHOC+S△PHB=$\frac{1}{2}$(OC+PH)•OH$+\frac{1}{2}$PH•BH
=$\frac{1}{2}OC•OH$$+\frac{1}{2}$PH(OC+BH)=$\frac{1}{2}OC•OH$$+\frac{1}{2}PH•OB$
=$\frac{1}{2}×4x+\frac{1}{2}$(-x2+3x+4)×4
=-2x2+8x+8
=-2(x-2)2+16
∴当x=2时,四边形PBOC的最大面积是16;
(3)∵点D(m,m+1)在第一象限的抛物线上,
∴m+1=-m2+3m+4,
∴m2-2m-3=0,
∴m=-1或m=3.
∵点D在第一象限,
∴点D的坐标为(3,4),
如图2,由(1)知,OB=OC=4,
∴∠OBC=45°,
设点D关于直线BC的对称点为点E,
∵C(0,4),∴CD∥AB且CD=3,
∴∠ECB=∠DCB=45°,
∴点E在y轴上,且CE=CD=3,
∴OE=1,
∴点E的坐标为(0,1).
即点D关于直线BC对称的点的坐标为(0,1).
点评 本题主要考查了二次函数的最值及抛物线与x轴的交点,能够根据二次函数的解析式得出各点坐标是解答此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
| A. | $\frac{10}{3}$cm | B. | $\frac{8}{3}$cm | C. | $\frac{5}{2}$cm | D. | $\sqrt{5}$cm |
| A. | 8.5×103亿元 | B. | 0.85×104亿元 | C. | 8.5×104亿元 | D. | 85×102亿元 |
| A. | 15 | B. | 30 | C. | $\sqrt{30}$ | D. | 15π |