题目内容
13. 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
分析 利用旋转的性质,旋转中心在各对应点的连线段的垂直平分线上,则作线段AD、BE、FC的垂直平分线,它们相点P(0,1)即为旋转中心.
解答 解:作线段AD、BE、FC的垂直平分线,它们相交于点P(0,1),如图,
所以△DEF是由△ABC绕着点P逆时针旋转90°得到的.
故选B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.解决本题的关键是利用旋转的性质确定旋转中心.

练习册系列答案
相关题目
5.某校初一学年对学生课桌数量进行统计,计划每班应有固定数量的课桌,实际比计划多记为“+”,实际比计划少记为“-”,以下是各班课桌数量的统计情况:
实际比计划的课桌数多还是少?多多少?或少多少?
| 班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
| 课桌 | -4 | -6 | -5 | +3 | -2 | +4 |
6.将多项式(2x+y)2-(x-2y)2分解因式的正确结果是( )
| A. | (3x+y)(x-3y) | B. | (3x-y)(x+3y) | C. | (3x-y)(x-3y) | D. | (3x+y)(x+3y) |
3.-3n=(-3)n成立的条件是( )
| A. | n为奇数 | B. | n是正整数 | C. | n是偶数 | D. | n是负数 |
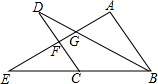 如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.
如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4. 如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.
如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.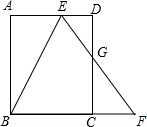 如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.
如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.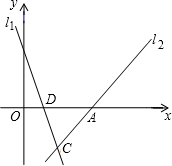 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.