题目内容
1.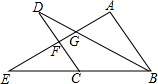 如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.
如图,AB∥CD,AB=CD=BC,点E是BC延长线上一点,连接AE,分别交BD、CD于点G、F,若AG=$\sqrt{5}$,GF=1,则EF=4.
分析 由平行四边形的性质可证明:△ADG∽△EBG,△DGF∽△BGA,得出和AG,EG,FG有关的比例式,即可得出AG2=EG•FG,代入数值计算即可求出EF的长.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BE,AB∥DF;
∴△ADG∽△EBG,△DGF∽△BGA,
∴$\frac{AG}{EG}=\frac{DG}{BG}$,$\frac{FG}{AG}=\frac{DG}{BG}$,
∴$\frac{AG}{EG}=\frac{FG}{AG}$,
∵AG=$\sqrt{5}$,GF=1,
∴AG2=EG•FG,
∴5=(EF+1)×1,
解得:EF=4,
故答案为:4.
点评 本题考查了平行四边形的性质、相似三角形的判定及其性质等知识;熟练掌握平行四边形的性质,由三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
13. 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
 如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长.
如图,将等腰三角形纸片ABC沿底边BC上的高AD剪成两个三角形,用这两个三角形你能拼成多少种平行四边形?试一试,分别求出它们的对角线的长. 如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒. 阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.
阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整. 数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.
数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.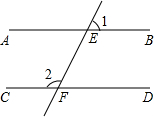 如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.
如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.