题目内容
5.(1)解不等式:|x-1|+|x-3|>4.(2)解关于x的不等式:x2-(1+a)x+a<0(a为常数)
分析 (1)由条件利用绝对值的意义求得不等式|x-1|+|x-3|>4的解集.
(2)不等式可变形为(x-1)(x-a)<0,分类讨论a的值的情况,求得不等式的解集.
解答 解:(1)|x-1|+|x-3|表示数轴上的x对应点到1、3对应点的距离之和,
而0和4对应点到1、3对应点的距离之和正好等于4,故|x-1|+|x-3|>4的解集为:{x|x<0,或x>4}.
(2)不等式可变形为(x-1)(x-a)<0.
∴当a>1时,原不等式的解为1<x<a;
当a=1时,原不等式的无实数解;
当a<1时,原不等式的解为:a<x<1.
点评 本题主要考查了绝对值的意义,绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
17.抛物线y=2x2+4x+1与x轴( )
| A. | 无交点 | B. | 只有一个交点 | ||
| C. | 有两个不同的交点 | D. | 有三个不同的交点 |
13. 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
20.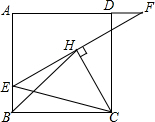 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )| A. | 5$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
15.一个正多边形的内角和与其外角和之和是1440°,则这个正多边形的一个外角的度数为( )
| A. | 36° | B. | 45° | C. | 55° | D. | 60° |
 阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.
阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整. 数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.
数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.