题目内容
8. 如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.
如图,⊙O中,AB,AC是弦,点M是$\widehat{CAB}$的中点,MP⊥AB,垂足为P,若AC=1,AP=2,则PB的长为4.
分析 首先证明△DEB、△AEC是等腰三角形,得到AE=AC=1,PE=PB=3,即可解决问题.
解答  解:如图,延长MP交⊙O于D,连接DB、DC,延长DC、BA交于点E,
解:如图,延长MP交⊙O于D,连接DB、DC,延长DC、BA交于点E,
∵$\widehat{CM}$=$\widehat{BM}$,
∴∠CDM=∠BDM,
∵PM⊥AB,
∴∠DPE=∠DPB=90°,
在△DPE和△DPB中,
$\left\{\begin{array}{l}{∠DPE=∠DPB}\\{DP=DP}\\{∠EDP=∠BDP}\end{array}\right.$,
∴△DPE≌△DPB,
∴DE=DB,EP=PB,
∴∠E=∠B,
∵∠ECA=∠B,
∴∠E=∠ECA,
∴AE=AC=1,
∵PA=2,
∴PE=PB=AE+PA=3,
∴AB=PB+PA=3+1=4.
故答案为4.
点评 本题考查圆周角定理、圆内接四边形的性质、等腰三角形的判定和性质、全等三角形的判定和性质等知识,利用等腰三角形的性质是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
13. 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
20.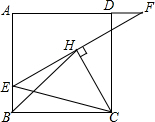 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )
如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且BE=DF,连接EF;作CH⊥EF,连接CE、BH,若BH=8,EF=4$\sqrt{10}$,则正方形ABCD的边长是( )| A. | 5$\sqrt{2}$ | B. | 6$\sqrt{2}$ | C. | 5$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
 阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.
阿春准备在如图所示的边长为1的正方形网格中,作一个三边长分别为4,5,$\sqrt{17}$的△ABC,他已经作出了其中的一条边,请你帮他把这个三角形补充完整.