题目内容
2.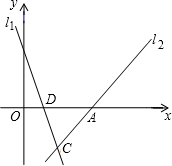 如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.
如图,已知直线l1:y=-3x+3与直线l2:y=mx-4m的图象的交点C在第四象限,且点C到y轴的距离为2.(1)求直线l2的解析式;
(2)求△ADC的面积.
分析 (1)只需根据条件先求出点C的坐标,然后代入y=mx-4m就可解决问题;
(2)只需求出点A、D的坐标,就可解决问题.
解答 解(1)∵点C到y轴距离为2,点C在直线l1上,
∴y=-3×2+3=-3.
∴点C(2,-3).
∵点C在直线l2上,
∴-3=2m-4m,
解得m=$\frac{3}{2}$,
∴l2的解析式为y=$\frac{3}{2}$x-6;
(2)∵点D是直线y=-3x+3与x轴的交点,
∴点D的坐标为(1,0).
∵点A是直线y=$\frac{3}{2}$x-6与x轴的交点,
∴点A的坐标为(4,0),
∴AD=4-1=3,
∴S△ADC=$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 本题主要考查的是两直线的交点问题、运用待定系数法求直线的解析式、直线上点的坐标特征、三角形的面积公式等知识,需要注意的是将线段的长度与坐标进行转换时要考虑纵横坐标的符号.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
13. 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
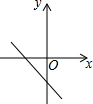
 数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.
数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.
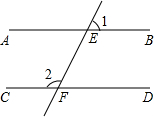 如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.
如图,已知AB∥CD,EF分别交AB、CD于点E、F,∠1=70°,则∠2的度数是110°.