题目内容
18.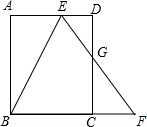 如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.
如图,矩形ABCD中,E是AD边上一点,F是BC延长线一点,EF交CD于点G,连接BE.若BE平分∠AEF,G是CD边的中点,tan∠ABE=$\frac{1}{2}$,则$\frac{DE}{AE}$的值为$\frac{3}{4}$.
分析 过点F作FM⊥BE,垂足为点M,根据角平分线的性质和矩形的性质得出BM=EM,再根据锐角三角函数的定义得出$\frac{AE}{AB}$=$\frac{1}{2}$,设AE=x,则AB=2x,求出BM,再根据三角形内角和定理得出∠ABE=∠BFM,求出BF,在△DEG和△CFG中,根据AAS长出△DEG≌△CFG,求出DE=CF,得出AD+CF=AE+DE+CF=AE+2DE,求出x的值,即可得出答案.
解答  解:过点F作FM⊥BE,垂足为点M,
解:过点F作FM⊥BE,垂足为点M,
∵BE平分∠AEF,
∴∠AEB=∠BEF,
∵AD∥BF,
∴∠AEB=∠EBF,
∴∠BEF=∠EBF,
∴FE=FB,
∴BM=EM,
∵tan∠ABE=$\frac{1}{2}$,
∴$\frac{AE}{AB}$=$\frac{1}{2}$,
设AE=x,则AB=2x,
∵∠A=90°,
∴BE=$\sqrt{5}$x,
∴BM=$\frac{\sqrt{5}}{2}$x,
∵∠ABE+∠EBF=90°,
∠BFM+∠EBF=90°,
∴∠ABE=∠BFM,
∴$\frac{BM}{FM}$=$\frac{1}{2}$,
∴FM=$\sqrt{5}$x,
∴BF=$\frac{5}{2}$x,
在△DEG和△CFG中,
$\left\{\begin{array}{l}{∠D=∠GCF}\\{∠DGE=∠CGF}\\{DG=CG}\end{array}\right.$,
∴△DEG≌△CFG,
∴DE=CF,
∵AD=BC,
∴AD+CF=AE+DE+CF=AE+2DE,
∴$\frac{5}{2}$x=x+2DE,
∴DE=$\frac{3}{4}$x,
∴$\frac{DE}{AE}$=$\frac{\frac{3}{4}x}{x}$=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$.
点评 此题考查了相似三角形的判定与性质,用到的知识点是矩形的性质、相似三角形的判定与性质、锐角三角函数、三角形内角和定理,关键是根据题意作出辅助线,证出BM=EM.

 如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )
如图,△DEF是由△ABC绕着某点旋转得到的,则这点的坐标是( )| A. | (1,1) | B. | (0,1) | C. | (-1,1) | D. | (2,0) |
 如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )
如图,将长为2a,宽为a的矩形纸片分割成n个三角形后,拼成面积为2a2的正方形,则下列关于n的说法错误的是( )| A. | n可以为3和4 | |
| B. | n可以为所有正偶数 | |
| C. | n可以为所有大于2的整数 | |
| D. | 正整数中所有3的倍数的数都可以为n值 |
| A. | 3 | B. | -3 | C. | 2 | D. | -1 |
 如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒.
如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P从点A出发沿射线AD方向以每秒1个单位的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位的速度运动,在线段QC上取点E,使得QE=2,连结PE,设点P的运动时间为t秒. 数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.
数a,b在数轴上的对应点的位置如图所示,化简|2b+a|-|b-a|=2a+b.