题目内容
13. △ABC的内切圆的三个切点分别为D、E、F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.
△ABC的内切圆的三个切点分别为D、E、F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.
分析 首先根据∠A=75°,∠B=45°,求出∠C=60°;然后根据△ABC的内切圆的三个切点分别为D、E、F,可得∠OEC=∠OFC=90°,再根据四边形OEFC的内角和等于360°,求出圆心角∠EOF的度数是多少即可.
解答 解:∵∠A=75°,∠B=45°,
∴∠C=180°-75°-45°
=105°-45°
=60°
∵△ABC的内切圆的三个切点分别为D、E、F,
∴∠OEC=∠OFC=90°,
∵四边形OECF的内角和等于360°,
∴∠EOF=360°-(90°+90°+60°)
=360°-240°
=120°
故答案为:120.
点评 此题主要考查了三角形的内切圆与内心,要熟练掌握,解答此题的关键是要明确:三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.

练习册系列答案
相关题目
4.我市飞鹤中学初三(一)班某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )
| A. | 30,27 | B. | 30,29 | C. | 29,30 | D. | 30,28 |
2.下列说法错误的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对边分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边相等,另一组对边平行的四边形是平行四边形 |
 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732) 小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
小宇在学习解直角三角形的知识后,萌生了测量他家对面位于同一水平面的楼房高度的想法,他站在自家C处测得对面楼房底端B的俯角为45°,测得对面楼房顶端A的仰角为30°,并量得两栋楼房间的距离为9米,请你用小宇测得的数据求出对面楼房AB的高度.(结果保留到整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)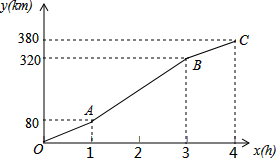 暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.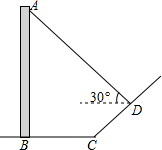 如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号)
如图,直立于地面上的电线杆AB,在阳光下落在水平地面和坡面上的影子分别是BC、CD,测得BC=6米,CD=4米,∠BCD=150°,在D处测得电线杆顶端A的仰角为30°,试求电线杆的高度(结果保留根号) 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:①∠ADG=22.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG;⑥若S△OGF=1,则正方形ABCD的面积是6+4$\sqrt{2}$,其中正确的结论个数为( )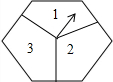 如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为$\frac{4}{9}$.
如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为$\frac{4}{9}$.