题目内容
3. 如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
如图,为了开发利用海洋资源,我勘测飞机测量钓鱼岛附属岛屿之一的北小岛(又称为鸟岛)两侧端点A,B的距离,飞机在距海平面垂直高度为100米的北小岛上方点C处测得端点A的俯角为30°,测得端点B的俯角为45°,求北小岛两侧端点A,B的距离(结果精确到1米,$\sqrt{3}$≈1.732)
分析 作CD⊥AB于D,根据正切的概念分别求出AD、BD的长,计算即可.
解答 解: 作CD⊥AB于D,
作CD⊥AB于D,
由题意得,∠A=30°,∠B=45°,CD=100米,
AD=$\frac{CD}{tanA}$=100$\sqrt{3}$,BD=CD=100,
∴AB=AD+BD=100$\sqrt{3}$+100≈273米,
答:小岛两侧端点A,B的距离约为273米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,当图形中没有直角三角形时,要通过作高或垂线构造直角三角形,另当问题以一个实际问题的形式给出时,要善于读懂题意,把实际问题划归为直角三角形中边角关系问题加以解决.

练习册系列答案
相关题目
11.不等式组$\left\{\begin{array}{l}{2x-1>0}\\{x+1≥0}\end{array}\right.$的解集是( )
| A. | x$>\frac{1}{2}$ | B. | -1$≤x<\frac{1}{2}$ | C. | x$<\frac{1}{2}$ | D. | x≥-1 |
18.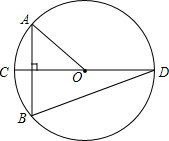 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
 如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )
如图,⊙O的直径CD垂直于弦AB,∠AOC=40°,则∠CDB的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
15.若a<b,则下列不等式成立的是( )
| A. | -a>-b | B. | -a+1>b+1 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac<bc |
12. 如图,AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )
如图,AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )
 如图,AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )
如图,AB∥CD,CE交AB于点F,若∠E=20°,∠C=45°,则∠A的度数为( )| A. | 15° | B. | 25° | C. | 35° | D. | 45° |
 如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).
如图,点A(2,0),以OA为半径在第一象限内作圆弧AB,使∠AOB=60°,点C为弧AB的中点,D为半径OA上一动点(不与点O,A重合),点A关于直线CD的对称点为E,若点E落在半径OA上,则点E的坐标为($2\sqrt{3}-2,0$);若点E落在半径OB上,则点E的坐标为($\sqrt{3}-1$,$3-\sqrt{3}$).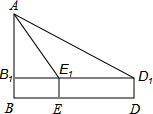 在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)
在一次课外实践活动中,老师要求同学们利用测角仪和皮尺估测教学楼AB的高度.同学们在教学楼的正前方D处用高为1米的测角仪测的教学楼顶端A的仰角为30°,然后他们向教学楼方向前进30米到达E处,又测得A的仰角为60°,则教学楼高度AB是多少米?(精确到0.1米,参考数据$\sqrt{3}$=1.732)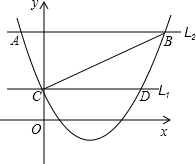 如图,抛物线F:y=ax2+bx+c(a>0)与y轴相交于点C,直线L1经过点C且平行于x轴,将L1向上平移t(t>0)个单位得到直线L2.设L1与抛物线F的交点为C、D,L2与抛物线F的交点为A、B,连结AC、BC.
如图,抛物线F:y=ax2+bx+c(a>0)与y轴相交于点C,直线L1经过点C且平行于x轴,将L1向上平移t(t>0)个单位得到直线L2.设L1与抛物线F的交点为C、D,L2与抛物线F的交点为A、B,连结AC、BC. △ABC的内切圆的三个切点分别为D、E、F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.
△ABC的内切圆的三个切点分别为D、E、F,∠A=75°,∠B=45°,则圆心角∠EOF=120度.