题目内容
6.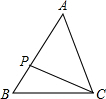 如图,P是△ABC的边AB上的一点.
如图,P是△ABC的边AB上的一点.(1)如果∠ACP=∠B,△ACP与△ABC是否相似?为什么?
(2)如果$\frac{AP}{AC}$=$\frac{AC}{AB}$,△ACP与△ABC是否相似?为什么?如果$\frac{AC}{CP}$=$\frac{BC}{AC}$呢?
分析 (1)由两角相等的三角形相似即可得出结论;
(2)由两边成比例且夹角相等,得出如果$\frac{AP}{AC}$=$\frac{AC}{AB}$,再由公共角相等得出△ACP与△ABC相似;如果$\frac{AC}{CP}$=$\frac{BC}{AC}$,但∠ACB≠∠ACP,得出△ACP与△ABC不一定相似.
解答 解:(1)△ACP∽△ABC;理由如下:
∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC;
(2)如果$\frac{AP}{AC}$=$\frac{AC}{AB}$,△ACP与△ABC相似;理由如下:
∵$\frac{AP}{AC}$=$\frac{AC}{AB}$,∠A=∠A,
∴△ACP与△ABC;
如果$\frac{AC}{CP}$=$\frac{BC}{AC}$,△ACP与△ABC不一定相似;理由如下:
∵$\frac{AC}{CP}$=$\frac{BC}{AC}$,但∠ACB≠∠ACP,
∴△ACP与△ABC不一定相似.
点评 本题考查了相似三角形的判定方法;熟练掌握相似三角形的判定方法,注意两边成比例且夹角相等的两个三角形相似.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
16.若a2+a=-1,则a4+a3-3a2-4a+3的值为( )
| A. | 7 | B. | 8 | C. | 10 | D. | 12 |
15.在一次读书活动中,某人从5本不同的科技书和7本不同的文艺书中任意选一本阅读,那么他选科技书的概率是( )
| A. | $\frac{5}{7}$ | B. | $\frac{5}{12}$ | C. | $\frac{7}{12}$ | D. | $\frac{7}{5}$ |
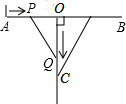 如图,线段AB=100cm,点O是AB的中点,射线OC垂直于AB,动点P以2cm/s的速度由A向B运动.同时,动点Q以3cm/s的速度由O沿射线OC运动,那么几秒后,△POQ的面积为450cm2?
如图,线段AB=100cm,点O是AB的中点,射线OC垂直于AB,动点P以2cm/s的速度由A向B运动.同时,动点Q以3cm/s的速度由O沿射线OC运动,那么几秒后,△POQ的面积为450cm2? 一个窗户的形状如图所示,如果窗户的用料是19米,则窗户面积y(m2)与宽x(m)间的函数关系式为y=-x2+6.5x,当边长x为3.25时,室内的光线最充足.(精确到0.1m)
一个窗户的形状如图所示,如果窗户的用料是19米,则窗户面积y(m2)与宽x(m)间的函数关系式为y=-x2+6.5x,当边长x为3.25时,室内的光线最充足.(精确到0.1m)