题目内容
19.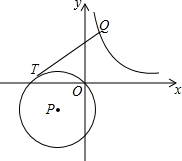 如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )
如图,在平面直角坐标系中,⊙P的圆心坐标是(-1,-1),半径为$\sqrt{2}$,点Q是函数y=$\frac{1}{x}$的图象上一动点,过点Q作⊙P的切线QT,切点为T,则线段QT长度的最小值为( )| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 4 |
分析 连接PT、PQ,由切线的性质可知△QTP为直角三角形,由PT为定值可知当QP有最小值时,线段QT长度的值最小.
解答 解:连接PT、PQ.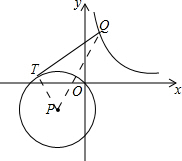
∵QT是⊙P的切线,
∴QT⊥PT.
∴QT=$\sqrt{Q{P}^{2}-T{P}^{2}}$.
设点Q的坐标为(x,$\frac{1}{x}$).
则QT=$\sqrt{(x+1)^{2}+(\frac{1}{x}+1)^{2}-(\sqrt{2})^{2}}$=$\sqrt{{x}^{2}+2x+\frac{1}{{x}^{2}}+\frac{2}{x}}$
当x=$\frac{1}{x}$时,$\sqrt{{x}^{2}+2x+\frac{1}{{x}^{2}}+\frac{2}{x}}$有最小值.
解得:x=±1.
∵点Q为与第一象限,
∴x=1.
∴线段QT长度的最小值=$\sqrt{{1}^{2}+2×1+\frac{1}{{1}^{2}}+\frac{2}{1}}$=$\sqrt{6}$.
故选:C.
点评 本题主要考查的是切线的性质、勾股定理的应用,明确当x=$\frac{1}{x}$时线段QT长度存在最小值是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
9. 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
 如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )
如图,已知点M为?ABCD的边AB的中点,线段CM交BD于点E,则图中阴影部分的面积与?ABCD面积的比是( )| A. | 1:2 | B. | 2:5 | C. | 3:5 | D. | 1:3 |
14.如果α是锐角,且cosα=$\frac{4}{5}$,那么sinα的值( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
4.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a-b+c=0,则方程一定有一个根为-1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有( )
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a-b+c=0,则方程一定有一个根为-1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③ | D. | ①②③④ |
8.方程x2+16=8x的根的情况为( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |