题目内容
15.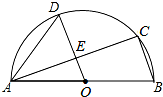 如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )
如图,AB是半圆O的直径,C、D是半圆O上的两点,OD∥BC,OD与AC交于点E.下列结论不一定成立的是( )| A. | △AOD是等边三角形 | B. | $\widehat{AD}$=$\widehat{CD}$ | ||
| C. | ∠ACB=90° | D. | OE=$\frac{1}{2}$BC |
分析 根据圆周角定理及垂径定理对各选项进行逐一分析即可.
解答 解:A、∵∠B的度数不确定,∴△AOD的形状无法确定,故本选项错误;
B、∵AB是半圆O的直径,∴∠C=90°.∵OD∥BC,∴∠AEO=90°,∴OD是AC的垂直平分线,∴$\widehat{AD}$=$\widehat{CD}$,故本选项正确;
C、∵AB是半圆O的直径,∴∠ACB=90°,故本选项正确;
D、∵OD∥BC,点O是AB的中点,∴OE是△ABC的中位线,∴OE=$\frac{1}{2}$BC,故本选项正确.
故选A.
点评 本题考查的是圆周角定理,熟知直径所对的圆周角是直角是解答此题的关键.

练习册系列答案
相关题目
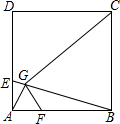 如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证:
如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证: 如图所示,在△ABC中,AD是它的角平分线,AB=7cm,AC=4cm,则S△ABD:S△ACD=7:4.
如图所示,在△ABC中,AD是它的角平分线,AB=7cm,AC=4cm,则S△ABD:S△ACD=7:4.