题目内容
9．已知二次函数y=ax2+bx+c，按要求分别写出一个二次函数的表达式：（1）满足条件：abc=0．
（2）满足条件：a+b+c＜0．
分析 （1）根据题意写出满足条件的a、b、c的值即可；
（2）根据题意写出满足条件的a、b、c的值．
解答 解：（1）y=x2+x，其中a=1，b=1，c=0，则abc=0；
（2）y=x2+x-3，其中a=1，b=1，c=-3，则a+b+c＜0．
点评 本题考查的是待定系数法求二次函数的解析式，根据题意给出a、b、c的值是解题的关键．
练习册系列答案
教材全解字词句篇系列答案
相关题目
17．
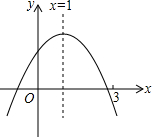二次函数y=ax2+bx+c（a≠0）图象如图所示．下列结论中，错误的是（ ）
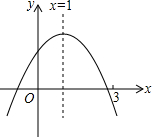二次函数y=ax2+bx+c（a≠0）图象如图所示．下列结论中，错误的是（ ）| A． | abc＜0 | |
| B． | 当m≠1时，a+b＞am2+bm | |
| C． | 2a+b=0 | |
| D． | 若ax12+bx1=ax22+bx2且x1≠x2，x1+x2=3 |
4．对于一元二次方程ax2+bx+c=0（a≠0），有下列说法：
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③ | D． | ①②③④ |
在一次抽奖活动中，主办方将奖品随机的放在如图所示的黑白相间的正方形小窗后，如果这次抽奖共分三等，其中一等奖1个，二等奖2相，三等奖3个，那么第一个抽奖人推开一扇黑色小窗能够得到一等奖奖品的概率为$\frac{1}{21}$．
18．已知三角形三条边的长度是三个连续的自然数，且它的周长小于18，符合上述条件的三角形有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
19．分解因式4mx-6my正确的是（ ）
| A． | m（4x-6y） | B． | 2m（2x+3y） | C． | 2m（2x-3y） | D． | 2m（2x-6y） |