题目内容
13．
如图，BD是△ABC的中线，AB=6cm，BC=4cm，则△ABD和△BCD的周长差为2cm．
分析 根据三角形的中线得出AD=CD，根据三角形的周长求出即可．
解答 解：∵BD是△ABC的中线，
∴AD=CD，
∴△ABD和△BCD的周长的差是：（AB+BD+AD）-（BC+BD+CD）=AB-BC=6-4=2cm．
故答案为：2．
点评 本题主要考查对三角形的中线的理解和掌握，能正确地进行计算是解此题的关键．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
4．对于一元二次方程ax2+bx+c=0（a≠0），有下列说法：
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
①当a＜0，且b＞a+c时，方程一定有实数根；
②若ac＜0，则方程有两个不相等的实数根；
③若a-b+c=0，则方程一定有一个根为-1；
④若方程有两个不相等的实数根，则方程bx2+ax+c=0一定有两个不相等的实数根．
其中正确的有（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③ | D． | ①②③④ |
8．方程x2+16=8x的根的情况为（ ）
| A． | 有两个不相等的实数根 | B． | 有两个相等的实数根 | ||
| C． | 有一个实数根 | D． | 没有实数根 |
18．已知三角形三条边的长度是三个连续的自然数，且它的周长小于18，符合上述条件的三角形有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图所示，在△ABC中，AD是它的角平分线，AB=7cm，AC=4cm，则S△ABD：S△ACD=7：4．
3．
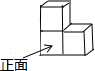如图，由三个小正方体搭成的几何体，这个几何体的左视图是（ ）
如图，由三个小正方体搭成的几何体，这个几何体的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |