题目内容
14.如图,∠ABC的两边分别平行于∠DEF的两边,且∠ABC=25°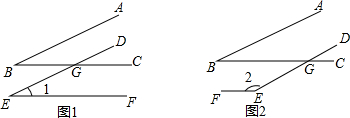
(1)∠1=25°,∠2=155°;
(2)观察∠1,∠2分别与∠ABC有怎样的关系,请你归纳出一个命题.
分析 (1)图1,根据平行线的性质,由AB∥DE得到∠B=∠DGC=25°,再由BC∥EF得∠1=∠DGC=25°;
图2,根据平行线的性质,由AB∥DE得∠B=∠BGE=25°,再由BC∥EF得∠2+∠BGE=180°,所以∠2=155°;
(2)由(1)的计算结果易得∠1与∠ABC相等,∠2与∠ABC互补,这个结论可归纳为:如果两个角的两边分别平行,那么这两个角相等或互补.
解答 解:(1)图1,∵AB∥DE,
∴∠B=∠DGC=25°,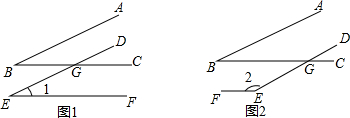
∵BC∥EF,
∴∠1=∠DGC=25°;
图2,
∵AB∥DE,
∴∠B=∠BGE=25°,
∵BC∥EF,
∴∠2+∠BGE=180°,
∴∠2=180°-25°=155°;
故答案为25°,155°;
(2)∠1与∠ABC相等,∠2与∠ABC互补,
结论:如果两个角的两边分别平行,那么这两个角相等或互补.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
4.对于一元二次方程ax2+bx+c=0(a≠0),有下列说法:
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a-b+c=0,则方程一定有一个根为-1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有( )
①当a<0,且b>a+c时,方程一定有实数根;
②若ac<0,则方程有两个不相等的实数根;
③若a-b+c=0,则方程一定有一个根为-1;
④若方程有两个不相等的实数根,则方程bx2+ax+c=0一定有两个不相等的实数根.
其中正确的有( )
| A. | ①②③ | B. | ①②④ | C. | ②③ | D. | ①②③④ |
19.分解因式4mx-6my正确的是( )
| A. | m(4x-6y) | B. | 2m(2x+3y) | C. | 2m(2x-3y) | D. | 2m(2x-6y) |
3.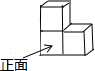 如图,由三个小正方体搭成的几何体,这个几何体的左视图是( )
如图,由三个小正方体搭成的几何体,这个几何体的左视图是( )
 如图,由三个小正方体搭成的几何体,这个几何体的左视图是( )
如图,由三个小正方体搭成的几何体,这个几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
 如图所示,在△ABC中,AD是它的角平分线,AB=7cm,AC=4cm,则S△ABD:S△ACD=7:4.
如图所示,在△ABC中,AD是它的角平分线,AB=7cm,AC=4cm,则S△ABD:S△ACD=7:4.